Topologie înseamnă. Sensul cuvântului topologie. Principalele etape în dezvoltarea topologiei

Conținutul articolului

TOPOLOGIE, ramură a matematicii care se ocupă de proprietățile figurilor (sau spațiilor) care sunt păstrate sub deformații continue, cum ar fi, de exemplu, tensiune, compresie sau îndoire. Deformarea continuă este o deformare a unei figuri, în care nu există rupturi (adică, încălcarea integrității figurii) sau lipire (adică identificarea punctelor sale). Astfel de proprietăți geometrice sunt legate de poziție și nu de forma sau dimensiunea figurii. Spre deosebire de geometriile euclidiene și riemanniene, geometria Lobachevsky și alte geometrii care se ocupă de măsurarea lungimilor și unghiurilor, topologia are un caracter nonmetric și calitativ. Anterior, era numită „analiza situației” (analiza poziției), precum și „teoria seturilor de puncte”. În literatura de specialitate, topologia este adesea denumită „geometrie a foii de cauciuc”, deoarece poate fi vizualizată ca geometria formelor desenate pe foi de cauciuc perfect elastice care sunt întinse, comprimate sau îndoite. Topologia este una dintre cele mai noi ramuri ale matematicii.

Poveste.

În 1640, filozoful și matematicianul francez R. Descartes (1596–1650) a găsit o relație invariabilă între numărul de vârfuri, muchii și fețe ale poliedrelor simple. Descartes a exprimat această relație prin formula V-E+F= 2, unde V este numărul de vârfuri, E este numărul de coaste și F este numărul de muchii. În 1752, matematicianul elvețian L. Euler (1707–1783) a dat o demonstrație riguroasă a acestei formule. O altă contribuție a lui Euler la dezvoltarea topologiei este soluția celebrei probleme a podului Königsberg. Era vorba despre o insulă de pe râul Pregel în Königsberg (în locul în care râul se împarte în două ramuri - Vechiul și Noua Pregel) și șapte poduri care leagă insula de malurile. Provocarea a fost de a afla dacă se poate ocoli toate cele șapte poduri într-un traseu continuu, vizitându-le pe fiecare o singură dată și revenind la punctul de plecare. Euler a înlocuit zonele de teren cu puncte și podurile cu linii. Euler a numit configurația rezultată un grafic, puncte - vârfurile sale și linii - muchii. El a împărțit vârfurile în par și impar, în funcție de faptul dacă un număr par sau impar de muchii iese din vârf. Euler a arătat că toate muchiile unui grafic pot fi parcurse exact o dată de-a lungul unui traseu închis continuu numai dacă graficul conține doar vârfuri pare. Deoarece graficul din problema podului Königsberg conține doar vârfuri impare, este imposibil să ocoliți podurile de-a lungul unui traseu continuu, vizitându-le pe fiecare exact o dată și revenind la începutul traseului.

Soluția propusă de Euler la problema podurilor Königsberg depinde doar de poziția relativă a podurilor. A marcat începutul formal al topologiei ca ramură a matematicii. K. Gauss (1777–1855) a creat teoria nodurilor, care a fost studiată ulterior de I. Listing (1808–1882), P. Tate (1831–1901) și J. Alexander. În 1840 A. Möbius (1790–1868) a formulat așa-numita problemă a patru culori, care a fost investigată ulterior de O. de Morgan (1806–1871) și A. Cayley (1821–1895). Prima lucrare sistematică asupra topologiei a fost Studii preliminare asupra topologiei Listare (1874).

Fondatorii topologiei moderne sunt G. Kantor (1845–1918), A. Poincaré (1854–1912) și L. Brouwer (1881–1966).

Secțiuni de topologie.

Topologia poate fi împărțită în trei domenii: 1) topologia combinatorie, care studiază formele geometrice prin descompunerea lor în forme simple care se alătură între ele într-un mod regulat; 2) topologia algebrică, care se ocupă cu studiul structurilor algebrice asociate spațiilor topologice, cu accent pe teoria grupurilor; 3) topologia teoretică a mulțimii, care studiază mulțimile ca colecții de puncte (spre deosebire de metodele combinatorii, care reprezintă un obiect ca o uniune de obiecte mai simple) și descrie mulțimile în termeni de proprietăți topologice precum deschiderea, închiderea, conexiunea etc. Desigur, o astfel de împărțire a topologiei în regiuni este oarecum arbitrară; mulți topologi preferă să evidențieze alte secțiuni în ea.

Câteva concepte de bază.

Spațiul topologic este format din multe puncte Sși o mulțime S de submulțimi ale mulțimii S, satisfacand urmatoarele axiome:

(1) întregul set S iar multimea goala apartine lui S;

(2) unirea oricărei colecții de mulțimi din S este o mulțime din S;

(3) intersecția oricărui număr finit de mulțimi din S este o mulțime din S.

Se numesc multimile incluse in multimea S seturi deschise, și acest set în sine este topologie V S. Cm. TEORIA SETURILOR.

Transformare topologică, sau homeomorfism, o figură geometrică S altcuiva Sў, este o mapare ( p ® pў) puncte p din S la puncte p¢ din S¢ care îndeplineşte următoarele condiţii: 1) corespondenţa stabilită de acesta între punctele din SȘi S¢ unu-la-unu, de ex. fiecare punct p din S doar un punct se potrivește p¢ din S¢ și la fiecare punct p¢ este afișat un singur punct p; 2) maparea este reciproc continuă (continuă în ambele direcții), adică dacă se acordă două puncte p, q din Sși punct p se deplasează în așa fel încât distanța dintre acesta și punct q tinde spre zero, apoi distanța dintre punctele corespunzătoare pў, q¢ din S¢ tinde, de asemenea, spre zero și invers.

Se numesc figuri geometrice care trec una în alta în timpul transformărilor topologice homeomorf. Cercul și limita unui pătrat sunt homeomorfe, deoarece pot fi transformate unul în altul printr-o transformare topologică (adică prin îndoire și întindere fără rupere sau lipire, de exemplu, prin întinderea limitei unui pătrat cu cercul circumscris în jurul acestuia). aceasta). Sfera și suprafața unui cub sunt, de asemenea, homeomorfe. Pentru a demonstra că figurile sunt homeomorfe, este suficient să indicăm transformarea corespunzătoare, dar faptul că nu putem găsi o transformare pentru unele figuri nu demonstrează că aceste figuri nu sunt homeomorfe. Proprietățile topologice ajută aici.

proprietate topologică(sau invariant topologic) a figurilor geometrice este o proprietate care, împreună cu o figură dată, este deținută și de orice figură în care trece în timpul unei transformări topologice.

Se apelează orice set deschis conectat care conține cel puțin un punct zonă.

O regiune în care orice curbă simplă închisă (adică, homeomorfă la un cerc) poate fi contractată la un punct, rămânând tot timpul în această regiune, se numește conectate individual pur și simplu conectat. Dacă, pe de altă parte, o curbă simplă închisă a acestei regiuni nu poate fi contractată la un punct în timp ce rămâne în această regiune tot timpul, atunci regiunea se numește multipli conectate, iar proprietatea corespunzătoare a zonei este multipli conectate. Imaginează-ți două regiuni circulare, sau discuri, una fără găuri și una cu găuri. Prima regiune este pur și simplu conectată, a doua este multimultiplicată. Pur și simplu conectat și multiplicat conectat sunt proprietăți topologice. O regiune cu o gaură nu poate trece sub un homeomorfism într-o regiune fără găuri. Este interesant de remarcat faptul că, dacă o tăietură este desenată într-un disc multiplu conectat de la fiecare dintre găuri până la marginea discului, atunci aceasta devine pur și simplu conectată.

Numărul maxim de curbe simple și închise, care nu se intersectează, de-a lungul cărora o suprafață închisă poate fi tăiată fără a o împărți în părți separate se numește prin naștere suprafete. Genul este un invariant topologic al unei suprafețe. Se poate dovedi că genul sferei este egal cu zero, genul torusului (suprafața „gogoșii”) este egal cu unu, genul covrigului (torus cu două găuri) este doi, genul de suprafata este de c p găuri este egală p. Acest lucru implică faptul că nici suprafața cubului, nici sferei nu sunt homeomorfe pentru tor.

Printre invarianții topologici ai unei suprafețe, se poate remarca și numărul de laturi și numărul de muchii. Un disc are 2 laturi, 1 muchie și genul 0. Un tor are 2 laturi, fără margini, iar genul său este 1.

Conceptele introduse mai sus fac posibilă rafinarea definiției topologiei: topologia este o ramură a matematicii care studiază proprietățile care se păstrează sub homeomorfisme.

Probleme și rezultate importante.

Teorema curbei închise a lui Jordan.

Dacă pe suprafață este trasată o curbă simplă închisă, există vreo proprietate a curbei care se păstrează atunci când suprafața este deformată? Existența unei astfel de proprietăți rezultă din următoarea teoremă: o curbă simplă închisă pe un plan împarte planul în două regiuni, interioară și exterioară. Această teoremă aparent trivială este evidentă pentru curbele de formă simplă, de exemplu, pentru un cerc; cu toate acestea, situația este diferită pentru liniile întrerupte închise complexe. Teorema a fost formulată și demonstrată pentru prima dată de K. Jordan (1838–1922); cu toate acestea, dovada lui Jordan s-a dovedit a fi defectuoasă. O dovadă satisfăcătoare a fost propusă de O. Veblen (1880–1960) în 1905.

Teorema punctului fix a lui Brouwer.

Lăsa D este o zonă închisă formată dintr-un cerc și interiorul acestuia. Teorema lui Brouwer afirmă că pentru orice transformare continuă care ia fiecare punct al domeniului D până la un punct din aceeași zonă, există un punct care rămâne fix sub această transformare. (Transformarea nu se presupune a fi unu-la-unu.) Teorema punctului fix a lui Brouwer este de un interes deosebit deoarece pare a fi teorema topologică cel mai frecvent utilizată în altă parte în matematică.

Problema celor patru culori.

Problema este aceasta: orice hartă poate fi colorată în patru culori, astfel încât oricare două țări care au o graniță comună să fie colorate în culori diferite? Problema cu patru culori este topologică, deoarece nici forma țărilor, nici configurația granițelor nu contează.

Conjectura că patru culori sunt suficiente pentru colorarea corespunzătoare a oricărei cărți a fost formulată pentru prima dată în 1852. Experiența a arătat că patru culori sunt într-adevăr suficiente, dar o demonstrație matematică riguroasă nu a putut fi obținută mai mult de o sută de ani. Și abia în 1976, K. Appel și V. Haken de la Universitatea din Illinois, după ce au petrecut mai mult de 1000 de ore de computer, au obținut succes.

Suprafețe unilaterale.

Cea mai simplă suprafață unilaterală este bandă Möbius, numit după A. Möbius, care și-a descoperit extraordinarele proprietăți topologice în 1858. Să ABCD(Fig. 2, A) este o bandă dreptunghiulară de hârtie. Dacă lipiți punctul A cu un punct B, și un punct C cu un punct D(Fig. 2, b), obțineți un inel cu o suprafață interioară, o suprafață exterioară și două margini. O parte a inelului (Fig. 2, b) poate fi colorat. Suprafața vopsită va fi delimitată de marginile inelului. Gândacul poate face o „circumnavigație” în jurul inelului, stând fie pe o suprafață pictată, fie nevopsită. Dar dacă banda este răsucită o jumătate de tură înainte de a lipi capetele și lipiți punctul A cu un punct C, A B Cu D, apoi obținem banda Möbius (Fig. 2, V). Această formă are o singură suprafață și o margine. Orice încercare de a colora doar o parte a benzii Möbius este sortită eșecului, deoarece banda Möbius are o singură față. Un gândac care se târăște de-a lungul mijlocului unei benzi Möbius (fără să traverseze marginile) se va întoarce la punctul său de plecare în poziția „cu susul în jos”. Când tăiați banda Möbius de-a lungul liniei mediane, aceasta nu se împarte în două părți.

Noduri.

Un nod poate fi gândit ca o bucată încâlcită de frânghie subțire cu capete legate, situată în spațiu. Cel mai simplu exemplu este să faceți o buclă dintr-o bucată de frânghie, să treceți unul dintre capetele acesteia prin buclă și să conectați capetele. Ca urmare, obținem o curbă închisă care rămâne topologic aceeași, indiferent de modul în care este întinsă sau răsucită, fără a rupe sau lipi puncte separate. Problema clasificării nodurilor după sistemul invarianților topologici nu a fost încă rezolvată.

"Inel" de topologie- aceasta este o topologie în care fiecare computer este conectat prin linii de comunicație doar cu alte două: de la unul primește doar informații și doar transmite către celălalt. Pe fiecare linie de comunicație, ca și în cazul unei stele, funcționează doar un emițător și un receptor. Acest lucru elimină nevoia de terminatoare externe.
Fiecare calculator retransmite (reia) semnalul, adică acționează ca un repetor, prin urmare atenuarea semnalului în întregul inel nu contează, importantă doar atenuarea dintre calculatoarele vecine ale inelului. În acest caz, nu există un centru clar definit, toate computerele pot fi la fel. Cu toate acestea, destul de des în ring este alocat un abonat special, care controlează schimbul sau controlează schimbul. Este clar că prezența unui astfel de abonat de control reduce fiabilitatea rețelei, deoarece eșecul acesteia paralizează imediat întregul schimb.
Conectarea noilor abonați la „ring” este de obicei complet nedureroasă, deși necesită oprirea obligatorie a întregii rețele pe durata conexiunii. Ca și în cazul topologiei „autobuz”, numărul maxim de abonați în inel poate fi destul de mare (1000 sau mai mult). O pereche răsucită sau o fibră optică este utilizată ca purtător în rețea. Mesajele circulă în jur.
O stație de lucru poate transmite informații către o altă stație de lucru numai după ce primește dreptul de a transmite (token), astfel încât coliziunile sunt excluse. Informațiile sunt transmise în jurul inelului de la o stație de lucru la alta, prin urmare, dacă un computer eșuează, dacă nu se iau măsuri speciale, întreaga rețea va eșua.
Topologia inelului este de obicei cea mai rezistentă la congestie, oferă o funcționare fiabilă cu cele mai mari fluxuri de informații transmise prin rețea, deoarece de obicei nu există conflicte în ea (spre deosebire de magistrală) și nu există un abonat central (spre deosebire de steaua). ).

Distribuția fizică sau logică a nodurilor de rețea. Topologia fizică definește legăturile fizice (canalele) dintre noduri. Topologia logică descrie posibilele conexiuni între nodurile de rețea. În rețelele locale, cele mai comune sunt trei ......

TOPOLOGIE- într-un sens larg, zona de matematică care studiază topologia. proprietăți diferă. matematica. și fizice obiecte. Intuitiv, la topologic includ proprietăți calitative, stabile, care nu se modifică odată cu deformațiile. Mat. formalizarea ideii de topologic proprietati ...... Enciclopedie fizică

TOPOLOGIE- Știința, studiul localităților. Dicționar de cuvinte străine incluse în limba rusă. Chudinov A.N., 1910. topologie (gr. topos loc, aria + ... ologie) o ramură a matematicii care studiază cele mai generale proprietăți ale formelor geometrice (proprietăți, nu ... ... Dicționar de cuvinte străine ale limbii ruse

TOPOLOGIE- TOPOLOGIA, ramură a matematicii care studiază proprietățile formelor geometrice care rămân neschimbate sub orice deformare, strângere, întindere, răsucire (dar fără goluri și lipire). O ceașcă cu mâner este echivalentă topologic cu un bagel; cub, ... ... Dicționar enciclopedic științific și tehnic

TOPOLOGIE- (din grecescul topos loc si ... logica) ramură a matematicii care studiază proprietățile topologice ale figurilor, adică proprietăți care nu se modifică sub nicio deformație produsă fără goluri și lipire (mai precis, cu unu-la- unul si continuu ...... Dicţionar enciclopedic mare

TOPOLOGIE- TOPOLOGIE, topologii, pl. nu, femeie (din greaca. loc topos si invatatura logos) (mat.). O parte a geometriei care studiază proprietățile calitative ale figurilor (adică, independent de concepte precum lungime, unghiuri, dreptate etc.). Dictionar… … Dicționar explicativ al lui Ushakov

topologie- substantiv, număr de sinonime: 1 matematică (29) Dicționar de sinonime ASIS. V.N. Trishin. 2013... Dicţionar de sinonime

Topologie- Topologia este o ramură a matematicii care studiază proprietățile formelor geometrice care nu se modifică la deformații care apar fără discontinuități. Dicţionar de termeni de afaceri. Akademik.ru. 2001... Glosar de termeni de afaceri

Topologie IC- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. Dicționar englez rus de inginerie electrică și inginerie energetică, Moscova, 1999] Subiecte de inginerie electrică, concepte de bază EN structura circuitului integrat ... Manualul Traducătorului Tehnic

Cărți

• Topology of skew products, N. Steenrod, Cititorului i se oferă o carte a celebrului matematician american Norman Steenrod, în care, pentru prima dată în literatura matematică, sunt prezentate, pe larg, bazele teoriei produselor skew... Categorie: Topologie Seria: Moștenire fizică și matematică: Matematică (Istoria matematicii) Editura: Librokom, Cumpărați pentru 568 de ruble
• Topologie pentru licențe de matematică. Manual, Ignatochkina Liya Anatolyevna, Manualul a fost scris de studenții din anul II ai MIGU, care studiau în direcția diplomei de licență „Matematică”. Într-o formă ușor de înțeles pentru studenții de licență,... Categoria: Științe matematice Editor:

Topologie- un cuvânt destul de frumos, sonor, foarte popular în unele cercuri nematematice, m-a interesat în clasa a IX-a. Desigur, nu aveam o idee exactă, însă bănuiam că totul era legat de geometrie.

Cuvintele și textul au fost alese astfel încât totul să fie „intuitiv clar”. Ca rezultat - o lipsă completă de alfabetizare matematică.

Ce este topologia ? Trebuie să spun imediat că există cel puțin doi termeni „Topologie” - unul dintre ei pur și simplu denotă o structură matematică, al doilea - poartă o întreagă știință. Această știință constă în studierea proprietăților unui obiect care nu se va schimba atunci când este deformat.

Exemplu ilustrativ 1. Cupa bagel.

Vedem că cana se transformă într-un bagel cu deformări continue (la oamenii de rând, un „tor bidimensional”). S-a observat că topologia studiază ceea ce rămâne neschimbat sub astfel de deformații. În acest caz, numărul de „găuri” din obiect rămâne neschimbat - este unul. Să lăsăm așa cum este deocamdată, ne dăm seama mai târziu)

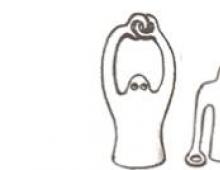
Exemplu ilustrativ 2. Omul topologic.

Cu deformări continue, o persoană (vezi figura) își poate desface degetele - un fapt. Nu este imediat evident, dar poți ghici. Și dacă omul nostru topologic pune cu prudență ceasul pe o mână, atunci sarcina noastră va deveni imposibilă.

Să fim clari

Deci, sper că câteva exemple au adus o oarecare claritate la ceea ce se întâmplă.
Să încercăm să oficializăm totul într-un mod copilăresc.
Vom presupune că lucrăm cu figuri de plastilină, iar plastilina poate întinderea, comprimarea, în timp ce lipirea diferitelor puncte și goluri sunt interzise. Figurile sunt numite homeomorfe, care sunt traduse unele în altele prin deformări continue descrise puțin mai devreme.

O carcasă foarte utilă este o sferă cu mânere. O sferă poate avea 0 mânere - atunci este doar o sferă, poate una - atunci este o gogoașă (în oamenii de rând „torul bidimensional”) etc.
Deci, de ce o sferă cu mânere se deosebește de alte figuri? Totul este foarte simplu - orice figură este homeomorfă unei sfere cu un anumit număr de mânere. Adică, de fapt, nu avem nimic altceva.O_o Orice obiect tridimensional este aranjat ca o sferă cu un anumit număr de mânere. Fie că este vorba de o ceașcă, lingură, furculiță (linguriță=furculiță!), mouse de computer, persoană.

Iată o teoremă atât de semnificativă demonstrată. Nu de noi, și nici acum. Mai exact, s-a dovedit pentru o situație mult mai generală. Să explic: ne-am limitat la luarea în considerare a figurilor turnate din plastilină și fără cavități. Acest lucru provoacă următoarele probleme:
1) nu putem obține o suprafață neorientabilă în niciun fel (sticlă Klein, bandă Möbius, plan proiectiv),
2) ne limităm la suprafețe bidimensionale (n/a: sferă - suprafață bidimensională),
3) nu putem obține suprafețe, figuri care se extind până la infinit (desigur că vă puteți imagina acest lucru, dar nicio plastilină nu este suficientă).

Fâșia Mobius

Sticla Klein

Dicționar explicativ al limbii ruse. D.N. Uşakov

topologie

topologie, pl. nu, w. (din greaca topos - loc si logos - invatatura) (mat.). O parte a geometriei care studiază proprietățile calitative ale figurilor (adică, independent de concepte precum lungime, unghiuri, dreptate etc.).

Noul dicționar explicativ și derivativ al limbii ruse, T. F. Efremova.

topologie

și. O ramură a matematicii care studiază proprietățile calitative ale figurilor geometrice care nu depind de lungimea lor, unghiuri, dreptate etc.

Dicţionar enciclopedic, 1998

topologie

TOPOLOGIA (din greaca. topos - loc si ... ologie) este o ramura a matematicii care studiaza proprietatile topologice ale figurilor, i.e. proprietăți care nu se modifică sub nicio deformație produsă fără discontinuități și lipiri (mai precis, sub mapări one-to-one și continue). Exemple de proprietăți topologice ale figurilor sunt dimensiunea, numărul de curbe care delimitează o zonă dată și așa mai departe. Deci, un cerc, o elipsă, un contur pătrat au aceleași proprietăți topologice, deoarece aceste linii pot fi deformate una în alta în modul descris mai sus; în același timp, inelul și cercul au proprietăți topologice diferite: cercul este delimitat de un contur, iar inelul de două.

Topologie

(din grecescul topos ≈ loc și ¼ logie) ≈ parte a geometriei dedicată studiului fenomenului de continuitate (exprimat, de exemplu, în conceptul de limită). O varietate de manifestări ale continuității în matematică și o gamă largă de abordări diferite ale studiului acesteia au condus la dezintegrarea unei singure teorii a matematicii într-un număr de departamente („teoria generală”, „teoria algebrică” etc.), care diferă unul de altul în materia și metoda de studiu și de fapt foarte puțin interconectate. I. Topologie generală Partea de teorie orientată spre studiul axiomatic al continuității se numește teorie generală.Alături de algebra, teoria generală formează baza metodei moderne de teorie a mulțimilor în matematică. Din punct de vedere axiomatic, continuitatea poate fi definită în multe moduri (în general vorbind, neechivalent). Axiomatica general acceptată se bazează pe conceptul unui set deschis. O structură topologică, sau topologie, pe o mulțime X este o astfel de familie de submulțimi, numite mulțimi deschise, încât: 1) mulțimea goală Æ și tot X sunt deschise; 2) uniunea oricărui număr și intersecția unui număr finit de mulțimi deschise este deschisă. O mulțime pe care este dată o structură topologică se numește spațiu topologic. Într-un spațiu topologic X se pot defini toate conceptele de bază ale analizei elementare legate de continuitate. De exemplu, o vecinătate a unui punct x О X este o mulțime deschisă arbitrară care conține acest punct; o mulţime A Ì X se numeşte închisă dacă complementul ei X \ A este deschis; închiderea unei mulțimi A este cea mai mică mulțime închisă care conține A; dacă această închidere coincide cu X, atunci A se spune că este dens peste tot în X și așa mai departe. Prin definiție, Æ și X sunt ambele mulțimi închise și deschise. Dacă nu există alte mulțimi în X care sunt simultan închise și deschise, atunci spațiul topologic X se spune că este conectat. Un spațiu conectat vizual este format dintr-o „piesă”, iar unul deconectat este format din mai multe. Orice submulțime A a unui spațiu topologic X are o structură topologică naturală constând din intersecții cu A de mulțimi deschise din X. Un A echipat cu această structură se numește subspațiu al spațiului X. vecinătatea sa e (bilă de rază e centrată pe acest punct). În special, orice submulțime a unui spațiu euclidian n-dimensional ═ este un spațiu topologic. Teoria unor astfel de spații (sub denumirea de „teoria geometrică”) și teoria spațiilor metrice sunt în mod tradițional incluse în teoria generală.Teoria geometrică este destul de clar împărțită în două părți: studiul submulților de complexitate arbitrară, sub rezerva anumitor restricții generale. (un exemplu se numește teoria continuumurilor, adică mulțimi închise mărginite conectate) și studiul modalităților în care spații topologice simple precum sfera, bila etc. pot fi încorporate în ═. (investițiile în, de exemplu, sfere pot fi foarte complexe). O acoperire deschisă a unui spațiu topologic X este o familie de mulțimi deschise, a căror unire este întregul lui X. Un spațiu topologic X se numește compact (în altă terminologie, ≈bicompact) dacă oricare dintre acoperirile sale deschise conține un finit. număr de elemente care formează și o acoperire. Teorema clasică Heine ≈ Borel afirmă că orice submulțime închisă mărginită este ═compact. Rezultă că toate teoremele principale ale analizei elementare despre mulțimi închise mărginite (de exemplu, teorema Weierstrass că o funcție continuă atinge valoarea maximă pe o astfel de mulțime) sunt valabile pentru orice spații topologice compacte. Aceasta definește rolul fundamental jucat de spațiile compacte în matematica modernă (în special în legătură cu teoremele de existență). Izolarea clasei de spații topologice compacte a fost una dintre cele mai mari realizări ale matematicii generale, care are o semnificație matematică generală. Se spune că un înveliș deschis (Vb) este înscris în (Ua) dacă pentru oricare b există o astfel încât Vb Ì Ua. Se spune că o acoperire (Vb) este local finită dacă fiecare punct x Î X are o vecinătate care intersectează doar un număr finit de elemente ale acestei acoperiri. Se spune că un spațiu topologic este paracompact dacă oricare dintre învelișurile sale deschise poate fi înscris cu o acoperire finită local. Clasa spațiilor paracompacte este un exemplu de clase de spații topologice obținute prin impunerea așa-numitelor condiții de tip compactitate. Această clasă este foarte largă; în special, conține toate spațiile topologice metrizabile, adică spațiile X în care este posibil să se introducă o metrică r astfel încât T. generat de r în X să coincidă cu T. dat în X. Multiplicitatea unui capac deschis este cel mai mare număr k astfel încât există k dintre elementele sale care au o intersecție nevidă. Cel mai mic număr n care are proprietatea că orice înveliș finit deschis al unui spațiu topologic X poate fi înscris cu un înveliș deschis de multiplicitate £n + 1 este notat cu simbolul dimX și se numește dimensiunea lui X. Această denumire este justificată de faptul că în situații geometrice elementare dimX coincide cu dimensiunea obișnuită înțeleasă, de exemplu dim = n. Sunt posibile și alte funcții numerice ale spațiului topologic X, diferite de dimX, dar în cele mai simple cazuri coincid cu dimX. Studiul lor este subiectul teoriei generale a dimensiunii, partea cea mai orientată geometric a T generalului. Numai în cadrul acestei teorii este posibil, de exemplu, să se dea o definiție clară și destul de generală a conceptului intuitiv al unei figuri geometrice și, în special, a conceptului de linie, suprafață etc. Clase importante de spații topologice se obțin prin impunerea așa-numitelor axiome de separabilitate. Un exemplu este așa-numita axiomă Hausdorff sau axioma T2, care necesită ca oricare două puncte distincte să aibă vecinătăți care nu se intersectează. Un spațiu topologic care satisface această axiomă se numește Hausdorff sau separabil. De ceva timp, aproape exclusiv spațiile Hausdorff au fost întâlnite în practica matematică (de exemplu, orice spațiu metric este Hausdorff). Cu toate acestea, rolul spațiilor topologice non-Hausdorff în analiză și geometrie este în continuă creștere. Spațiile topologice care sunt subspații ale spațiilor (bi)compacte Hausdorff sunt numite spații complet regulate sau spații Tihonov. Ele pot fi, de asemenea, caracterizate printr-o anumită axiomă de separabilitate, și anume, o axiomă care necesită ca pentru orice punct x0 ═X și orice mulțime închisă F ═X care nu o conține, să existe o funcție continuă g: X ╝ , egală cu zero la x0 și unul pe F. Spațiile topologice care sunt subspații deschise ale spațiilor Hausdorff compacte se numesc spații local compacte. Ele se caracterizează (în clasa spațiilor Hausdorff) prin faptul că fiecare dintre punctele lor are o vecinătate cu închidere compactă (exemplu: spațiu euclidian). Orice astfel de spațiu este completat de un punct pentru a-l face compact (exemplu: adunând un punct din plan, se obține sfera unei variabile complexe, iar din ═≈ sfera S n). O mapare f: X ╝ Y dintr-un spațiu topologic X la un spațiu topologic Y se numește mapare continuă dacă, pentru orice mulțime deschisă V Ì Y, mulțimea f≈1(V) este deschisă în X. O mapare continuă se numește un homeomorfism dacă este unul la unu și maparea inversă f≈ 1: Y ╝ X este continuă. O astfel de mapare stabilește o corespondență unu-la-unu între mulțimi deschise de spații topologice X și Y, permutabilă cu operațiile de unire și intersecție a mulțimilor. Prin urmare, toate proprietățile topologice (adică proprietățile formulate în termeni de mulțimi deschise) ale acestor spații sunt aceleași, iar din punct de vedere topologic, spațiile topologice homeomorfe (adică spații pentru care există cel puțin un homeomorfism X ╝ Y) ar trebui considerată la fel (la fel ca în geometria euclidiană figurile care pot fi combinate prin mișcare sunt considerate la fel). De exemplu, cercul și limita unui pătrat, hexagon etc. sunt homeomorfe („topologic la fel”). În general, oricare două linii închise simple (fără puncte duble) sunt homeomorfe. Dimpotrivă, un cerc nu este homeomorf la o dreaptă (deoarece eliminarea unui punct nu rupe conexiunea cercului, ci rupe conexiunea dreptei; din același motiv, linia dreaptă nu este homeomorfă cu planul , iar cercul nu este homeomorf la „opt”). De asemenea, cercul nu este homeomorf cu planul (aruncați nu unul, ci două puncte). Fie (Xa) ≈ o ​​familie arbitrară de spații topologice. Se consideră mulțimea X a tuturor familiilor de forma (хa), unde xa ═Xa (produsul direct al mulțimilor Xa). Pentru orice a, formula definește o mapare ═ (numită proiecție). În general vorbind, în X pot fi introduse multe structuri topologice sub care toate hărțile pa sunt continue. Printre aceste structuri, există cea mai mică (adică conținută în orice astfel de structură). Mulțimea X înzestrată cu această structură topologică se numește produsul topologic al spațiilor topologice Xa și se notează prin simbolul ПХa (și în cazul unui număr finit de factori, prin simbolul X1 ` ... ` Xn). În mod explicit, mulțimile deschise ale lui X pot fi descrise ca uniunea intersecțiilor finite ale tuturor mulțimilor de forma în care Ua este deschisă în Xa. Spațiul topologic X are următoarea proprietate remarcabilă de universalitate, care îl caracterizează în mod unic (până la homeomorfism): pentru orice familie de mapări continue fa: Y ╝ Xa, există o mapare continuă unică f: Y ╝ X pentru care ══pentru toate A. Spațiul ═este produsul topologic al n instanțe ale liniei reale. Una dintre cele mai importante teoreme ale teoriei generale este afirmația că produsul topologic al spațiilor topologice compacte este compact. Dacă X ≈ un spațiu topologic și Y ≈ o mulțime arbitrară și dacă este dată o mapare p: X ╝ Y a spațiului X pe mulțimea Y ​​(de exemplu, dacă Y este o mulțime de factori ai X printr-o relație de echivalență, iar p este o proiecție naturală care mapează fiecărui element al lui x н X clasa sa de echivalență), atunci putem pune problema introducerii în Y a unei structuri topologice în raport cu care maparea p este continuă. Cea mai „bogată” (în mulțimi deschise) o astfel de structură se obține presupunând că toate mulțimile V Ì Y sunt mulțimi deschise în Y pentru care mulțimea f‑1(V) Ì X este deschisă în X. Mulțimea Y ​​dotată cu aceasta structura topologică se numește spațiul coeficient al spațiului topologic X (față de p). Are proprietatea că o mapare arbitrară f: Y ╝ Z este continuă dacă și numai dacă maparea ═: X ╝ Z este continuă X. O mapare continuă p: X ╝ Y se numește deschisă dacă pentru orice mulțime deschisă U Ì X mulțimea p(U) este deschisă în Y și închisă dacă pentru orice mulțime închisă F Ì X mulțimea p(F) este închisă în Y. Ca mapări continue deschise și închise f: X ╝ Y pentru care f(X) = Y sunt factoriali. Fie X ≈ un spațiu topologic, A ≈ subspațiul său și f: A ╝ Y ≈ o hartă continuă. Presupunând că spațiile topologice X și Y sunt disjunctive, introducem o structură topologică în uniunea lor X È Y, considerând uniunile de mulțimi deschise din X și Y ca fiind mulțimi deschise. În continuare, introducem în spațiul X È Y cele mai mici. relație de echivalență în care a ~ f(a) pentru orice punct a Î A. Spațiul coeficient corespunzător se notează cu X È fY și se spune că se obține prin lipirea unui spațiu topologic X de un spațiu topologic Y față de A prin intermediul unei hărți continue f. Această operație simplă și vizuală se dovedește a fi foarte importantă, deoarece permite obținerea unora mai complexe din spații topologice relativ simple. Dacă Y constă dintr-un singur punct, atunci spațiul X È fY este notat cu X/A și se spune că se obține din X prin contractarea lui A la un punct. De exemplu, dacă X ≈ un disc și A ≈ cercul său de limită, atunci X/A este homeomorf unei sfere. 2. Topologie uniformă Partea de teorie care studiază conceptul axiomatic al continuității uniforme se numește teorie uniformă.Definiția continuității uniforme a funcțiilor numerice cunoscute din analiză poate fi transferată direct în mapările oricăror spații metrice. Prin urmare, axiomatica continuității uniforme se obține de obicei pornind de la spații metrice. Sunt studiate în detaliu două abordări axiomatice ale continuității uniforme, bazate, respectiv, pe conceptele de proximitate și împrejurimile diagonalei. Submulțimile A și B ale spațiilor metrice X se numesc apropiate (notația AdB) dacă pentru orice e > 0 există puncte a Î A și b Î B, distanța dintre care< e. Принимая основные свойства этого отношения за аксиомы, приходят к следующему определению: (отделимой) структурой близости на множестве Х называется такое отношение d на множестве всех его подмножеств, что: 1) ÆX (символом обозначается отрицание отношения d; 2) AB1 и AB2Û A(B1 U B2); ═3) {x}{y} Û x ¹ y;4) если АВ, то существует такое множество С В, что А(Х\С). Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости Х в пространство близости Y называется близостно непрерывным, если образы близких в Х множеств близки в Y. Пространства близости Х и Y называются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение X ╝ Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Т. эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество u Ì x открытым, если {x}(X \U) для любой точки х Î U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства Х все структуры близости на X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии ≈ би-компактными расширениями) вХ ≈ компактными хаусдорфовыми топологическими пространствами, содержащими Х в качестве всюду плотного пространства. Структура близости d, соответствующая расширению вХ, характеризуется тем, что АdВ тогда и только тогда, когда замыкания множеств А и В пересекаются в bX. В частности, на любом компактном хаусдорфовом топологическом пространстве Х существует единственная структура близости, порождающая его топологическую структуру. Другой подход основан на том, что равномерную непрерывность в метрическом пространстве Х можно определить в терминах отношения «точки х и у находятся на расстоянии, не большем e». С общей точки зрения, отношение на Х есть не что иное как произвольное подмножество U прямого произведения Х ` X. Отношение «тождество» является с этой точки зрения диагональю D Ì Х ` X, то есть множеством точек вида (х, х), х Î X. Для любого отношения U определено обратное отношение U≈1 = {(х, у); (у, х) Î U } и для любых двух отношений U и V определена их композиция U × V = {(х, у); существует z Î Х такое, что (х, z) Î U, (z, y) Î V }. Семейство отношений {U } называется (отделимой) равномерной структурой на Х (а отношения U называется окружениями диагонали), если: 1) пересечение любых двух окружений диагонали содержит окружение диагонали; 2) каждое окружение диагонали содержит D, и пересечение всех окружений диагонали совпадает с D; 3) вместе с U окружением диагонали является и U≈1; 4) для любого окружения диагонали U существует такое окружение диагонали W, что W o W Ì U. Множество, наделённое равномерной структурой, называется равномерным пространством. Отображение f: X ╝ Y равномерного пространства Х в равномерное пространство Y называется равномерно непрерывным, если прообраз при отображении f ` f: Х ` Х ╝ Y ` Y любого окружения диагонали V Ì Y ` Y содержит некоторое окружение диагонали из Х ` X. Равномерные пространства Х и Y называются равномерно гомеоморфными, если существует взаимно однозначное равномерно непрерывное отображение Х ╝ Y, обратное к которому также является равномерно непрерывным отображением. В равномерной Т. такие равномерные пространства считаются одинаковыми. Каждая равномерная структура на Х определяет некоторую структуру близости: АdВ тогда и только тогда, когда (A ` В) Ç U ¹ Æ для любого окружения диагонали U Ì X ` X. При этом равномерно непрерывные отображения оказываются близостно непрерывными. 3. Topologie algebrică Fie fiecare spațiu topologic X (din o clasă) să fie asociat cu un obiect algebric h(X) (grup, inel etc.), și fiecare mapare continuă f: X ╝ Y ≈ un anumit homomorfism h(f) : h( X) ╝ h(Y) (sau h(f) : h(Y) ╝ h(X), care este homomorfismul identităţii când f este harta identităţii. Dacă h(f1 ═f2) = h(f1) ═h( f2 ) (sau, respectiv, h(f1 ═f2) = h(f2) h(f1), atunci spunem că h este un functor (respectiv, un cofunctor). Majoritatea problemelor din teoria algebrică sunt legate într-un fel sau altul cu următoarea problemă de propagare: pentru o mapare continuă dată f: A ╝ Y a unui subspațiu A Ì X într-un spațiu topologic Y, găsiți o mapare continuă g: X ╝ Y care coincide cu f pe A, adică astfel încât f = g×i, unde i: A ╝ X ≈ maparea de încorporare (i(a) = a pentru orice punct a н A). Dacă o astfel de mapare continuă g există, atunci pentru orice functor (cofunctor) h există un homomorfism ( j: h(X) ╝ h(Y) (homomorfism j: h(Y) ╝ h(X)), astfel încât h(f) = j ═h(i) (respectiv, h(f) = h(i) ) ═j); va fi homomorfismul j = h(g). În consecință, inexistența homomorfismului j (pentru cel puțin un functor h) implică inexistența mapării g. De fapt, aproape toate metodele algebricei T pot fi reduse la acest principiu simplu, de exemplu, există un functor h a cărui valoare pe bila E n este trivială, iar pe sfera S n≈1 ≈ un grup netrivial pe sferă. S limitând mingea. Aceasta implică deja absența așa-numitei retractii ≈ mapare continuă p: E n╝ S n≈1, fixată pe S n≈1, adică astfel încât compoziția р×i, unde i: S n-1 ╝ E n ≈ embedding mapping , este maparea identității (dacă p există, atunci maparea identității grupului h(S n≈1) va fi compoziția mapărilor h(i) : h(S n≈1) ╝ h (E n) și h(p) : h( E n) ╝ h(S n≈1), ceea ce este imposibil pentru grupul trivial h(E n)). Cu toate acestea, acest fapt esențial geometric-elementar și (pentru n = 2) clar evident (însemnând din punct de vedere fizic posibilitatea de a trage un tambur pe un cerc rotund) nu a fost încă dovedit fără utilizarea metodelor algebric-topologice. Consecința sa imediată este afirmația că orice mapare continuă f: E n╝ E n are cel puțin un punct fix, adică ecuația f(x) = x are cel puțin o soluție în E n (dacă f(x) ¹ x pentru din toate x О E n, atunci, luând pentru p(x) un punct din S n≈1 coliniar la punctele f(x) și x și astfel încât segmentul cu capete f(x) și p(x) conţine x, obţinem retragerea p: E n╝ S n≈1). Această teoremă de punct fix a fost una dintre primele teoreme din teoria algebrică și mai târziu a devenit sursa unei serii întregi de diverse teoreme de existență pentru soluții la ecuații. În general, stabilirea inexistenței homomorfismului (j) este cu atât mai ușoară, cu atât structura algebrică a obiectelor h(X) este mai complexă.De aceea, în T. algebric, sunt considerate obiecte algebrice de natură extrem de complexă și cerinţele topologiei algebrice au stimulat semnificativ dezvoltarea algebrei abstracte.Spaţiul topologic X se numeşte spaţiu celular, precum şi o partiţie celulară (sau un complex CW), dacă conţine o succesiune crescândă de subspaţii X 0 Ì 0 Ì X n≈1 Ì X n Ì 0 (numite scheletele spațiului celular X), a cărui unire este întregul lui X și sunt îndeplinite următoarele condiții: 1) mulțimea U Ì X este deschisă în X dacă și numai dacă pentru orice n mulţimea U Ç X n este deschisă în X n; 2) X n se obține din X n≈1 prin lipirea unei familii de bile n-dimensionale de-a lungul sferelor lor (n≈1)-dimensionale (prin intermediul unei mapări continue arbitrare a acestor sfere în X n≈1); 3) X0 este format din puncte izolate. Astfel, structura spațiului celular constă, grosier vorbind, în faptul că acesta este reprezentat ca o unire de mulțimi homeomorfe cu bile deschise (aceste mulțimi se numesc celule). În T. algebric, spațiile celulare sunt studiate aproape exclusiv, întrucât specificitatea problemelor T. algebric pentru ele este deja pe deplin manifestată. Mai mult, de fapt, pentru T. algebric, unele spații celulare deosebit de simple (de tipul poliedrelor, vezi mai jos) prezintă interes, dar îngustarea clasei de spații celulare, de regulă, complică semnificativ studiul (din moment ce multe operaţiile utile asupra spaţiilor celulare sunt derivate din clasa poliedrelor). Două mapări continue f, g: X ╝ Y sunt numite homotopice dacă pot fi deformate continuu una în cealaltă, adică dacă există o familie de mapări continue ft: X ╝ Y continuu în funcție de parametrul t н astfel încât f0= f și f1 = g (dependența continuă de t înseamnă că formula F(x, t) = ft(x), x н X, t н definește o mapare continuă F: X ` ╝ Y; această mapare, precum și familia (ft ) se numește o homotopie care leagă f la g). Colecția tuturor mapărilor continue X ╝ Y se împarte în clase de homotopie de mapări reciproc homotopice. Setul de clase de homotopie de mapări continue de la X la Y este notat cu simbolul . Studiul proprietăților relației de homotopie și, în special, a mulțimilor este subiectul așa-numitei topologii de homotopie (sau teoria homotopiei). Pentru majoritatea spațiilor topologice interesante, mulțimile sunt finite sau numărabile și pot fi calculate în mod explicit eficient. Se spune că spațiile topologice X și Y sunt echivalente homotopic, sau având același tip de homotopie, dacă există hărți continue f: X ╝ Y și g: Y ╝ X astfel încât hărțile continue g×f: X ╝ X și f×g : Y ╝ Y sunt homotopice la mapările de identitate corespunzătoare. Într-o teorie a homotopiei, astfel de spații ar trebui să fie considerate identice (toți „invarianții de homotopie” lor coincid). Rezultă că în multe cazuri (în special, pentru spațiile celulare) solubilitatea problemei de propagare depinde doar de clasa de homotopie a hărții continue f: A ╝ Y; mai precis, dacă f are extensia g: X ╝ Y, atunci pentru orice homotopie ft: A ╝ Y (cu f0 = f) există o extensie gt: X ╝ Y astfel încât g0 = g. Prin urmare, în loc de f, putem considera clasa sa de homotopie [f] și, în consecință, studiem numai functorii (cofunctori) invarianți de homotopie h, adică astfel încât h(f0) = h(f1) dacă hărțile f0 și f1 sunt homotopice . Acest lucru duce la o împletire atât de strânsă a teoriei algebrice și homotopice, încât acestea pot fi considerate ca o singură disciplină. Pentru orice spațiu topologic Y, formulele h(X) = și h(f) = , unde f: X1 ╝ X2 și j: X2 ╝ Y, definesc un cofunctor invariant de homotopie h, despre care se spune că este reprezentat de spațiul topologic Y. Aceasta este ≈ este o metodă standard (și în esență singura) pentru construirea cofunctorilor invarianți de homotopie. Pentru ca mulțimea h(X) să se dovedească a fi, să zicem, un grup, trebuie să alegem Y într-un mod adecvat, de exemplu, trebuie să fie un grup topologic (în general vorbind, acest lucru nu este în întregime adevărat: este este necesar să se aleagă un punct x0 în X și să se ia în considerare doar mapări și homotopii continue, transformând x0 în unitatea grupului; această complicație tehnică va fi însă ignorată în cele ce urmează). Mai mult, este suficient ca Y să fie un grup topologic „în sensul de homotopie”, adică ca axiomele asociativității și existența unui element invers (afirmând că unele mapări coincid de fapt) să țină doar „până la homotopie”. Astfel de spații topologice sunt numite spații H. Astfel, fiecare H-spațiu Y definește un cofunctor homotopic invariant h(X) = ale cărui valori sunt grupuri. În mod similar (“dual”), fiecare spațiu topologic Y definește, prin formulele h(X) = , h(f) = , unde f: X1 ╝ X2 și j: Y ╝ X1, un functor h. Pentru ca h(X) să fie un grup, Y trebuie să aibă o anumită structură algebrică, într-un sens bine definit structura duală a unui spațiu H. Spațiile topologice dotate cu această structură sunt numite co-H-spații. Un exemplu de co-H-spațiu este sfera n-dimensională S n (pentru n ³ 1). Astfel, pentru orice spațiu topologic X, formula pnX = definește un grup pnX, n ³ 1, care se numește a n-a grupă de homotopie a spațiului X. Pentru n = 1, coincide cu grupul fundamental. Pentru n > 1 grupul pnX este comutativ. Dacă p1X= (1), atunci X se numește simplu conex. Un spațiu celular X se numește spațiu K(G, n) dacă pi(X) = 0 pentru i ¹ n și pnX = G; un astfel de spațiu celular există pentru orice n ³ 1 și orice grup G (commutativ pentru n > 1) și este definit în mod unic până la echivalența homotopiei. Pentru n > 1 (și, de asemenea, pentru n = 1, dacă grupul G este comutativ), spațiul K(G, n) se dovedește a fi un spațiu H și, prin urmare, reprezintă un grup H n(X; G) = . Acest grup este numit grupul de coomologie n-dimensional al unui spațiu topologic X cu grupul de coeficienți G. Este un reprezentant tipic al unui număr de cofunctori importanți, printre care se numără, de exemplu, functorul K KO(X) = [X , BO], reprezentată de așa-numitul BO Grassmannian infinit-dimensional, grupul de cobordism orientat WnX etc. Dacă G este un inel, atunci suma directă H*(X; G) a grupurilor H n(X; G) este o algebră peste G. Mai mult, această sumă directă are o structură algebrică foarte complexă, în care (pentru G = Zp, unde Zp ≈ grup ciclic de ordin p) include acțiunea asupra H*(X; G) a unei algebre necomutative p, numită algebra Steenrod. Complexitatea acestei structuri face posibilă, pe de o parte, dezvoltarea unor metode eficiente (dar deloc simple) de calcul a grupurilor H n(X; G), iar pe de altă parte, stabilirea legăturilor între grupele H. n(X; G) și alți functori invarianți de homotopie (de exemplu, , grupuri de homotopie pnX), care fac adesea posibilă calcularea acestor functori în mod explicit. Din punct de vedere istoric, grupurile de coomologie au fost precedate de așa-numitele grupuri de omologie Hn(X; G), care sunt grupurile de homotopie pnM(X, G) ale unui spațiu celular M(X, G) construit unic din spațiul celular X și grupa G. Grupurile de omologie și coomologie sunt într-un anumit sens duale între ele, iar teoriile lor sunt în esență echivalente. Cu toate acestea, structura algebrică care există în grupurile de omologie este mai puțin familiară (de exemplu, aceste grupuri nu constituie o algebră, ci o așa-numită coalgebră) și, prin urmare, grupurile de coomologie sunt de obicei utilizate în calcule. În același timp, în unele întrebări, grupurile de omologie se dovedesc a fi mai convenabile, deci sunt și ele studiate. Partea teoriei algebrice care se ocupă cu studiul (și aplicarea) grupurilor de omologie și coomologie se numește teoria omologiei. Extinderea rezultatelor teoriei algebrice la spații mai generale decât spațiile celulare este subiectul așa-numitei teorii algebrice generale.În special, teoria omologiei generale studiază grupurile de omologie și coomologie ale spațiilor topologice arbitrare și aplicațiile acestora. Se dovedește că în afara clasei de spații celulare compacte, abordări diferite ale construcției acestor grupuri conduc, în general, la rezultate diferite, astfel încât pentru spațiile topologice necelulare apar o serie de grupuri diferite de omologie și coomologie. Principala aplicație a teoriei omologiei generale este în teoria dimensiunii și în teoria așa-numitelor legi ale dualității (care descriu relația dintre proprietățile topologice a două submulțimi suplimentare ale unui spațiu topologic), iar dezvoltarea sa a fost în mare măsură stimulat de nevoile acestor teorii. 4. Topologie liniară pe bucăți O submulțime Р О ═ se numește con cu vârful a și baza В dacă fiecare dintre punctele sale aparține unui singur segment de forma ab, unde b О В. O mapare continuă f: X ╝ Y a poliedrelor se numește liniară pe bucăți dacă este liniară pe razele fiecărei vecinătăți conice a oricărui punct x Î X. O mapare liniară pe bucăți unu-la-unu a cărei inversă este, de asemenea, liniară pe bucăți se numește a izomorfism liniar pe bucăți. Subiectul teoriei liniare pe bucăți este studiul poliedrelor și al mapărilor lor liniare pe bucăți. În teoria liniară pe bucăți, poliedrele sunt considerate identice dacă sunt izomorfe liniar pe bucăți. O submulțime Х О ═este un poliedru (compact) dacă și numai dacă este uniunea unei familii (finite) de politopi convexi. Orice poliedru poate fi reprezentat ca o uniune de simplexe care se intersectează numai de-a lungul fețelor întregi. O astfel de reprezentare se numește triangularea poliedrului. Fiecare triangulație este determinată în mod unic de schema ei simplială, adică de mulțimea tuturor vârfurilor sale, în care sunt marcate submulțimile, care sunt mulțimi de vârfuri ale simplexurilor. Prin urmare, în loc de poliedre, se pot lua în considerare doar scheme simple ale triangulațiilor lor. De exemplu, conform schemei simple, se pot calcula grupele de omologie și coomologie. Aceasta se face astfel: a) un simplex ale cărui vârfuri sunt ordonate într-un anumit fel se numește simplex ordonat al triangulației (sau schemei simpliale) dată K; combinațiile liniare formale de simplexuri ordonate de o dimensiune n dată cu coeficienți dintr-un grup dat G se numesc lanțuri n-dimensionale; toate formează un grup în mod natural, care este notat cu simbolul C n(K; G); b) eliminând vârful cu numărul i, 0 £ i £ n din simplexul n-dimensional ordonat s, obținem un simplex (n≈1)-dimensional ordonat, care se notează cu simbolul s(i); lanțul ═ se numește limita lui s; prin liniaritate, maparea ═ se extinde la un homomorfism ═: Cn(K; G) ╝ Cn-1 (K; G); c) lanţurile c pentru care ═= 0 se numesc cicluri, formează grupul de cicluri Zn(K; G); d) lanțurile de forma ═ se numesc limite, formează grupul de limită Bn(K; G); e) demonstrați că Bn(K; G) Ì Zn(K; G) (limita este un ciclu); prin urmare, grupa de coeficient Hn(K; G) = Zn(K; G)/Bn(K; G) este definită. Rezultă că grupul Hn(K; G) este izomorf cu grupul de omologie Hn(X; G) al poliedrului X a cărui triangulație este K. O construcție similară, în care se începe nu de la lanțuri, ci de la colanțuri (funcții arbitrare definite pe mulțimea tuturor simplexelor ordonate și luând valori în G), dă grupuri de coomologie. Cu această construcție, prezentată aici într-o formă ușor modificată, a început formarea esențial algebricii T. În construcția inițială au fost luate în considerare așa-numitele simplexe orientate (clase de simplexe ordonate care diferă în permutări pare ale vârfurilor). Această construcție a fost dezvoltată și generalizată într-o mare varietate de direcții. În special, aspectele sale algebrice au dat naștere așa-numitei algebre omologice. În modul cel mai general, o schemă simplială poate fi definită ca o mulțime în care sunt marcate unele submulțimi finite („simplice”) și este necesar ca orice submulțime a unui simplex să fie din nou un simplex. O astfel de schemă simplială este o schemă simplă de triangulare a unui poliedru dacă și numai dacă numărul de elemente ale unei submulțimi marcate arbitrare nu depășește un număr fix. Totuși, conceptul de poliedru poate fi generalizat (prin obținerea așa-numitelor „poliedre cu dimensiuni infinite”), iar atunci orice schemă simplială va fi deja o schemă de triangulare a unui poliedru (numită realizarea lui geometrică). O acoperire deschisă arbitrară (Ua) a fiecărui spațiu topologic X poate fi asociată cu o schemă simplială ale cărei vârfuri sunt elementele Ua ale acoperirii și a cărei submulțime este marcată dacă și numai dacă elementele acoperirii care alcătuiesc această submulțime au un -intersectia goala. Această schemă simplă (și poliedrul corespunzător) se numește acoperire nervoasă. Nervii tuturor învelișurilor posibile aproximează într-un anumit sens spațiul X și, pornind de la grupele lor de omologie și coomologie, se pot obține, trecând la limita corespunzătoare, grupele de omologie și coomologie ale lui X. Această idee stă la baza aproape tuturor construcțiilor. a teoriei omologiei generale. Aproximarea unui spațiu topologic de către nervii învelișurilor sale deschise joacă, de asemenea, un rol important în teoria generală. 5. Topologia varietatilor Un spațiu topologic paracompact Hausdorff este numit o varietate topologică n-dimensională dacă este „local euclidian”, adică dacă fiecare dintre punctele sale are o vecinătate (numită vecinătate de coordonate sau hartă) homeomorfă spațiului topologic. Punctele din această vecinătate sunt date de n numere x1, ┘, xn, numite coordonate locale. La intersecția a două hărți, coordonatele locale corespunzătoare sunt exprimate unele prin altele prin intermediul unor funcții numite funcții de tranziție. Aceste funcții definesc un homeomorfism de mulțimi deschise în, numit homeomorfism de tranziție. Suntem de acord să numim un homeomorfism arbitrar între mulțimi deschise din ═ un t-homeomorfism. Un homeomorfism care este un izomorfism liniar pe bucăți va fi numit p-homeomorfism, iar dacă este exprimat prin funcții netede (diferențiabile de orice număr de ori), ≈ s-homeomorfism. Fie a = t, p sau s. O varietate topologică se numește a-varietate dacă acoperirea sa de diagrame este aleasă astfel încât homeomorfismele de tranziție pentru oricare două dintre diagramele sale (în intersectare) să fie a-homeomorfisme. O astfel de acoperire definește o structură a pe o varietate topologică X. Astfel, o varietate t ≈ este pur și simplu orice varietate topologică, varietățile p sunt numite varietăți liniare pe bucăți. Fiecare varietate liniară pe bucăți este un poliedru. În clasa tuturor poliedrelor, varietățile liniare în bucăți n-dimensionale sunt caracterizate prin faptul că oricare dintre punctele lor are o vecinătate izomorfă liniar în bucăți cu cubul n-dimensional. Varietățile s sunt numite varietăți netede (sau diferențiabile). O mapare a unei varietăți a se numește o mapare continuă arbitrară pentru a = t, o mapare liniară arbitrară pe bucăți pentru a = s ≈, o mapare netedă arbitrară pentru a = s ≈, adică o mapare continuă scrisă în local coordonate prin funcții netede. O mapare a unu-la-unu, a cărei inversă este și o mapare a, se numește a-homeomorfism (pentru a = s și difeomorfism), a-varietățile X și Y sunt numite a-homeomorfism (pentru a = s ≈ difeomorf) dacă există cel puțin un a-homeomorfism X ╝ Y. Subiectul teoriei a-varietăților este studiul a-varietăților și a-hărților lor; aici se presupune că varietățile a-homeomorfe sunt aceleași. Teoria soiurilor s este o parte a T liniar pe bucăți. Teoria soiurilor s se mai numește și T neted. Principala metodă a teoriei varietăților moderne este de a reduce problemele sale la probleme de T algebric. pentru unele spații topologice construite corespunzător. Această legătură strânsă între teoria varietăților și teoria algebrică a făcut posibilă, pe de o parte, rezolvarea multor probleme geometrice dificile și, pe de altă parte, a stimulat puternic dezvoltarea teoriei algebrice în sine.Exemple de varietăți netede sunt n- suprafețe dimensionale în , care nu au puncte singulare. Se dovedește (teorema de încorporare) că orice varietate netedă este difeomorfă la o astfel de suprafață (pentru N ³ 2n + 1). Un rezultat similar este valabil și pentru a = t, p. Fiecare p-varietate este o t-varietate. Se dovedește că pe orice varietate s se poate introduce o structură p (de obicei numită triangulație Eighthead) într-un mod natural. Putem spune că orice a-varietate unde a = p sau s este o a▓-varietate unde a▓ = t sau p. Răspunsul la întrebarea inversă: pe care a▓-variete poate fi introdusă o structură a (o astfel de a▓-varietate pentru a▓ = p se numește netezire, iar pentru a▓ = t ≈ triangulată), iar dacă este posibil, câți? ≈ depinde de dimensiunea n. Există doar două varietati topologice unidimensionale: cercul S1 (varietatea compactă) și linia dreaptă ═ (varietatea necompactă). Pentru orice a = p, s, există o structură a unică pe varietățile t S1 și ═. În mod similar, pe orice varietate (suprafață) topologică bidimensională există o structură a unică și toate suprafețele conectate compacte pot fi descrise cu ușurință (pot fi descrise și suprafețele conectate necompacte, dar răspunsul este mai complicat). Pentru ca suprafețele să fie homeomorfe, este suficient ca acestea să fie echivalente homotopic. Mai mult, tipul de homotopie al oricărei suprafețe este caracterizat în mod unic de grupele sale de omologie. Există două tipuri de suprafețe: orientabile și neorientabile. Orientabilii includ sfera S2 și torul T2. Fie X și Y ≈ două varietati a n-dimensionale conectate. Să tăiem o minge în X și Y (pentru n = 2 ≈ disc) și să lipim sferele de limită rezultate (pentru n = 2 ≈ cercuri). Cu unele precauții evidente, rezultatul este din nou o varietate a. Se numește suma conexă a a-varietăților X și Y și se notează cu X#Y. De exemplu, T2#T2 arată ca un covrig. Sfera S n este zero al acestei adunări, adică S n#X = X pentru orice X. În special, S2#T2= T2. Se dovedește că o suprafață orientabilă este homeomorfă la o sumă conexă de forma S2#T2#┘#T2, iar numărul p de termeni din T2 se numește genul suprafeței. Pentru o sferă p = 0, pentru un tor p = 1 etc. e. O suprafață din genul p poate fi vizualizată ca o sferă de care sunt lipite p „mânere”. Fiecare suprafață neorientabilă este homeomorfă la suma conexă P2# 0 #P2 a unui număr de planuri proiective P2. Poate fi considerată ca o sferă de care sunt lipite mai multe benzi Möbius. Pe fiecare 3-varietate topologică, pentru orice a = p, s, există, de asemenea, o structură a unică și toate tipurile de 3-variete topologice pot fi descrise (cu toate acestea, grupurile de omologie nu mai sunt suficiente pentru aceasta). În același timp, până în prezent (1976) nu au fost descrise toate varietățile topologice tridimensionale (cel puțin compacte conectate) de un anumit tip de homotopie. Acest lucru nu se face nici măcar pentru varietati pur și simplu conectate (toate sunt echivalente homotopic cu sfera S 3). Conjectura Poincaré afirmă că orice astfel de varietate este homeomorfă pentru S 3. Pentru varietățile topologice cu patru dimensiuni (compacte și conectate), problema existenței și unicității structurilor a (a = p, s) nu a fost încă rezolvată, iar tipul lor de homotopie este descris numai sub ipoteza că sunt pur și simplu conectate. Nu se știe dacă analogul conjecturii Poincare este valabil pentru ei. Este remarcabil că pentru varietăți topologice compacte și conectate de dimensiunea n ³ 5 situația se dovedește a fi complet diferită: toate problemele principale pentru acestea pot fi considerate rezolvate în principiu (mai precis, reduse la probleme de teorie algebrică). Orice colector neted X este încorporat ca o suprafață netedă (n-dimensională) în; iar vectorii tangenți la X constituie o nouă varietate netedă TX, care se numește pachetul tangent al unei varietăți netede X. În general, un pachet vectorial peste un spațiu topologic X este un spațiu topologic E pentru care o mapare continuă p: E ╝ X este dat astfel încât pentru fiecare punct x Î X preimaginea v (stratul) este un spațiu vectorial și există o acoperire deschisă (Ua) a lui X astfel încât pentru orice preimagine p≈1(Ua) este homeomorfă cu Ua ` , și există un homeomorfism p≈1(Ua) ╝ Ua ` , mapând liniar fiecare strat p≈1(x), x О Ua, pe spațiul vectorial (х) ` . Pentru E = TX, maparea continuă p asociază cu fiecare vector tangent punctul său de tangență, astfel încât stratul p≈1(x) va fi tangenta spațiului la X în punctul x. Rezultă că orice mănunchi de vectori peste un spațiu compact X definește un element al grupului KO(X). Astfel, în special, pentru orice colector X neted, compact și conectat, grupul KO(X) are un element corespunzător mănunchiului tangent. Se numește invariant tangențial al unei varietăți netede X. Există un analog al acestei construcții pentru orice a. Pentru a = p, rolul grupului KO(X) este jucat de un alt grup, care este notat cu KPL(X), iar pentru a = t, rolul acestui grup este jucat de grupul, notat cu KTop (X). Fiecare a-varietate X definește în grupul corespunzător [KO(X), KPL(X) sau KTop(X)] un element numit invariantul său a-tangențial. Există homomorfisme naturale KO(X) ╝ KPL(X) ╝ KTop(X), și se dovedește că pe un n-dimensional (n ³ 5) compact și conectat a"-varietate X, unde a" = t, p , atunci abia atunci putem introduce o structură a (a = p dacă a "= t și a = s dacă a" = p) când invariantul său "-tangențial se află în imaginea grupului corespunzător. Numărul de astfel de structuri este finită și egală cu numărul de elemente ale unei mulțimi de factori a mulțimii, unde Ya ≈ un spațiu topologic special construit (pentru a = s, spațiul topologic Ya este de obicei notat cu simbolul PL/O, iar pentru a = p ≈ prin simbolul Top/PL).Astfel, problema existenței și unicității structurii a- se reduce la o anumită problemă a teoriei homotopiei.Tipul de homotopie a spațiului topologic PL/O este destul de complicat și nu a avut încă a fost calculat complet (1976), dar se știe că pi(PL/O) = 0 pentru i £ 6, ceea ce implică faptul că orice varietate liniară pe bucăți de dimensiunea n £ 7 este netezibilă și unic pentru n £ 6. În contrast , tipul de homotopie al spațiului topologic Top/PL s-a dovedit a fi surprinzător de simplu: acest spațiu este homotopie echivalent cu K(ℤ2, 3). În consecință, numărul de structuri liniare pe bucăți dintr-o varietate topologică nu depășește numărul de elemente ale grupului H 3(X, ℤ2). Astfel de structuri există cu siguranță dacă H 4(X, ℤ2) = 0, dar pentru H 4(X, ℤ2) ¹ 0 este posibil să nu existe o structură liniară pe bucăți. În special, există o structură liniară unică pe bucăți pe sfera S n. Pot exista multe structuri netede pe sfera Sn, de exemplu, există 28 de structuri netede diferite pe S7. Pe torul T n (produsul topologic al n instanțe ale cercului S 1) există pentru n ³ 5 multe structuri liniare pe bucăți diferite, toate care admit o structură netedă. Astfel, începând de la dimensiunea 5, există varietăți netede homeomorfe, dar nu difeomorfe; sfere cu această proprietate există pornind de la dimensiunea 7. Este firesc să se rezolve problema descrierii (până la un a-homeomorfism) a tuturor n-dimensionale (n ³ 5) a-varietăți compacte conectate în două etape: să se caute condiții pentru echivalența homotopică a varietăților a și condițiile a-homeomorfisme ale varietăților a echivalente homotopic. Prima problemă ține de homotopia T. și poate fi considerată complet rezolvată în cadrul acesteia. A doua problemă este, de asemenea, în esență complet rezolvată (cel puțin pentru a-varietățile simple conectate). Baza soluției sale este transferul la dimensiuni mai mari a tehnicii de „descompunere a mânerului”. Cu ajutorul acestei tehnici, este posibil, de exemplu, să se demonstreze conjectura Poincare pentru varietăți topologice n-dimensionale (n ³ 5) (o varietate topologică compactă conectată care este echivalentă homotopic cu o sferă este homeomorfă cu aceasta). Alături de a-varietățile, se pot considera așa-numitele a-varietăți cu graniță; ele sunt caracterizate prin faptul că vecinătățile unora dintre punctele lor (constituind limita) sunt a-homeomorfe semispațiului Xn ³ 0 al spațiului. Granița este o varietate a (n≈1)-dimensională (în general, deconectată). Două varietati a compacte n-dimensionale X și Y sunt numite (co)bordante dacă există o varietate a compactă (n+1)-dimensională cu granița W, astfel încât granița ei să fie uniunea unor varietăți netede disjunse a-homeomorfe cu X și Y Dacă hărțile de încorporare X ╝ W și Y ╝ W sunt echivalențe de homotopie, atunci se spune că varietățile netede sunt h-cobordante. Folosind metode de descompunere cu mâner, se poate demonstra că, pentru n ³ 5, varietatile a compacte pur și simplu conectate sunt a-homeomorfe dacă sunt h-cobordante. Această teoremă h-cobordism oferă cea mai puternică modalitate de a stabili a-homeomorfismul a-varietăților (în special, conjectura Poincaré este o consecință a acesteia). Un rezultat similar, dar mai complicat, este valabil și pentru varietatile a neconectate simplu. Mulțimea ═claselor de a-varietăți compacte cobordante este un grup comutativ în raport cu operarea unei sume conexe. Zeroul acestui grup este clasa a-varietăților care sunt muchii, adică cobordante cu zero. Se pare că pentru a = s acest grup este izomorf cu grupul de homotopie p2n+1MO (n+1) al unui spațiu topologic MO (n+1) special construit, numit spațiu Thoma. Un rezultat similar este valabil pentru a = p, t. Prin urmare, metodele teoriei algebrice fac posibilă, în principiu, calcularea grupului. În special, se dovedește că grupul ═este o sumă directă a grupurilor ℤ2 în valoare egală cu numărul de partiții ale numărului n în alți termeni decât numerele de forma 2m≈

De exemplu, = 0 (deci fiecare varietate netedă compactă tridimensională este o limită). Dimpotrivă, ═= ℤ2, astfel încât să existe suprafețe cobordante între ele și nu cobordante cu zero; o astfel de suprafață, de exemplu, este planul proiectiv P

M. M. Postnikov.

6. Principalele etape în dezvoltarea topologiei

Rezultate separate de natură topologică au fost obținute încă din secolele al XVIII-lea și al XIX-lea. (Teorema lui Euler asupra poliedrelor convexe, clasificarea suprafețelor și teorema lui Jordan conform căreia o dreaptă simplă închisă situată într-un plan împarte planul în două părți). La începutul secolului al XX-lea se creează un concept general de spațiu în T. (metric ≈ M. Frechet, topologic ≈ F. Hausdorff), apar ideile inițiale ale teoriei dimensiunii și se demonstrează cele mai simple teoreme privind mapările continue (A. Lebesgue, L. Brouwer). ), se introduc poliedre (A. Poincaré) și se determină așa-numitele numere Betti ale acestora. Primul sfert al secolului XX culminează cu înflorirea matematicii generale și crearea școlii topologice de la Moscova; se pun bazele teoriei generale a dimensiunii (P. S. Uryson); axiomaticii spatiilor topologice i se da forma sa moderna (P. S. Aleksandrov); se construiește o teorie a spațiilor compacte (Aleksandrov, Uryson) și se demonstrează o teoremă asupra produsului lor (A. N. Tikhonov); sunt date pentru prima dată condițiile necesare și suficiente pentru metrizabilitatea unui spațiu (Aleksandrov, Uryson); introduce (Aleksandrov) noţiunea de acoperire local finită [pe baza căreia, în 1944, J. Dieudonné (Franţa) a definit spaţiile paracompacte]; sunt introduse spații complet regulate (Tikhonov); conceptul de nerv este definit și astfel se întemeiază teoria generală a omologiei (Aleksandrov). Sub influența lui E. Noether, numerele Betti sunt recunoscute ca rânduri ale grupurilor de omologie, care sunt, prin urmare, numite și grupuri Betti. L. S. Pontryagin, pe baza teoriei sale a caracterelor, demonstrează legile dualității pentru mulțimi închise.

În al 2-lea sfert al secolului al XX-lea. dezvoltarea termodinamicii generale și teoria omologiei continuă: A. Stone (SUA) și E. Cech introduc așa-numita piatră ≈ cehoviană, sau extinderea maximă, (bi)compactă, a unui spațiu complet regulat în dezvoltarea lui Tikhonov. idei; Sunt definite grupuri de omologie ale spațiilor arbitrare (cehă), se introduce multiplicarea în grupuri de coomologie (J. Alexander, A. N. Kolmogorov) și se construiește un inel de coomologie. La acea vreme, în teoria algebrică domnea metodele combinatorii, bazate pe luarea în considerare a schemelor simple; prin urmare, teoria algebrică este uneori și încă se numește teorie combinatorie.Se introduc spațiile de proximitate și spațiile uniforme. Teoria homotopiei începe să se dezvolte intens (H. Hopf, Pontryagin); Sunt definite grupuri de homotopie (V. Gurevich, SUA), iar pentru a le calcula sunt folosite considerațiile unei topografii netede (Pontriagin). Sunt formulate axiomele grupărilor de omologie și coomologie (N. Steenrod și S. Eilenberg, SUA). Apare teoria fasciculelor (H. Whitney, SUA; Pontryagin); sunt introduse spații celulare (J. Whitehead, Marea Britanie).

În a doua jumătate a secolului al XX-lea. în URSS se conturează școala sovietică de teorie generală și teoria omologiei: se lucrează la teoria dimensiunilor, problema metrizării, teoria extensiilor (bi)compacte și teoria generală a mapărilor continue (factoriale, deschise, etc.). și închis), în special, teoria absolutelor; teoria așa-numitelor invarianți cu valori cardinale (A.V. Arkhangel'skii, B.A. Pasynkov, V.I. Ponomarev, E.G. Sklyarenko, Yu.M. Smirnov și alții).

Prin eforturile unui număr de oameni de știință (J. P. Serre și A. Cartan în Franța, M. M. Postnikov în URSS, Whitehead și alții), teoria homotopilor prinde în sfârșit contur. În acest moment, au fost create centre mari de matematică algebrică în SUA, Marea Britanie și alte țări; Interesul pentru geometria geometrică este reînnoit.Se creează teoria fasciculelor vectoriale și a functorului K (M. Atiyah, Marea Britanie; F. Hirzebruch, Germania de Vest), geometria algebrică este utilizată pe scară largă în geometria netedă (R. Thom, Franța) și geometrie algebrică (Hirzebruch); se dezvoltă teoria (co)bordismelor (V. A. Rokhlin, URSS; Tom, S. P. Novikov) și teoria netezirii și triangulației (J. Milnor, SUA).

Dezvoltarea tehnologiei continuă în toate direcțiile, iar domeniul de aplicare al aplicațiilor sale este în continuă expansiune.

A. A. Maltsev.

═Lit.: Aleksandrov P.S., Introducere în teoria generală a mulțimilor și funcțiilor, M.≈L., 1948; Parkhomenko A.S., Ce este o linie, M., 1954; Pontryagin L. S., Fundamentele topologiei combinatorii, Moscow≈L., 1947; propriul său, Grupuri continue, ed. a III-a, M., 1973; Milnor J., Wallace A., Topologie diferențială. Curs elementar, trad. din engleză, M., 1972; Steenrod N., Chinn W., Primele concepte de topologie, trad. din engleză, M., 1967; P. S. Aleksandrov, Topologie combinatorie, Moscow≈L., 1947; Alexandrov P. S., Pasynkov B. A., Introducere în teoria dimensiunii. Introducere în teoria spațiilor topologice și teoria generală a dimensiunii, M., 1973; Alexandrov P. S., Introducere în teoria dimensiunii omologice și topologia combinatorie generală, Moscova, 1975; Arkhangelsky A. V., Ponomarev V. I. Fundamentele topologiei generale în probleme și exerciții, M., 1974; Postnikov M. M., Introducere în teoria lui Morse, M., 1971; Bourbaki N., Topologie generală. Structuri de bază, trad. din franceză, Moscova, 1968; lui, Topologie generală. Grupuri topologice. Numere și grupuri și spații aferente, trad. din franceză, Moscova, 1969; lui, Topologie generală. Utilizarea numerelor reale în topologia generală. spatii functionale. Rezumatul rezultatelor. Dicţionar, trans. din franceză, Moscova, 1975; Kuratovsky K., Topologie, trad. din engleză, vol. 1≈2, M., 1966≈69; Leng S., Introducere în teoria varietăților diferențiabile, trad. din engleză, M., 1967; Spanier E., Topologie algebrică, trad. din engleză, M., 1971.

Topologie (dezambiguizare)

Topologie:

• Topologia este o ramură a matematicii care studiază fenomenul continuității în forma sa cea mai generală.
• Topologia este un sistem de mulțimi utilizat în definirea unui spațiu topologic.
• Topologia rețelei - o diagramă a locației și conexiunii dispozitivelor de rețea.

Exemple de utilizare a cuvântului topologie în literatură.

Pontryagin, ale cărui eforturi au creat o nouă ramură a matematicii - algebra topologică - studiind diferite structuri algebrice înzestrate cu topologie.

Și nu se poate înțelege histologia fără hidrologie, hidrologie fără geologie, geologie fără geografie, geografie fără topografie, topografie fără topologieși toate împreună fără omneologie, și omneologie - fără tabele.

Nu am înțeles histologia, nu am înțeles hidrologia, hidrografia, geografia, topografia, topologie.

În general, această abordare presupune documentarea rețelei topologie, programe de aplicație și protocoale utilizate.

Așa că a continuat, folosind termeni din ce în ce mai complicati, referindu-se la topologie spiritul și geometria realizărilor și intuițiilor, conturând elementele ontografiei endoscopice, climatizarea vieții emoționale, nivelurile sale, extreme, suișuri și coborâșuri, precum și depresiuni ale spiritului, și a vorbit atât de mult încât a fost răgușit, iar regele avea dureri de cap.

Carduri topologie rutarea corespondenței este utilă pentru rezolvarea problemelor legate de transferul de corespondență între servere.

De asemenea, sperăm să vedem o bibliotecă de rezoluție de nivel superior care sortează răspunsurile pe baza informațiilor despre topologie, care există doar pe gazda clientului.

Aceasta înseamnă că rețeaua topologie iar segmentarea devine un factor important de securitate.

La urma urmei, în esență, orice teorie se reduce la topologie imagini, iar orice ontologie nu este altceva decât un complex deductiv de imagini universale legate inductiv de realitatea empirică.

A crea topologie servere la distanță, mai întâi determinați bazele de date pe care stațiile de lucru și serverele le vor accesa cel mai frecvent.

Și anume, în lumea continuum topologie conexiunile sale interne permit să se constituie un mediu în care intersubiectivitatea devine o funcție a distribuției raționalităților în cadrul acesteia.

Adică, potrivit obiectivistului topologie lume corpusculară, problema intersubiectivității este rezolvată în ea cu ajutorul unui mediator intersubstanțial.

Este vorba despre unii topologii spații care se încadrează unul în celălalt, se întorc unul în celălalt, așa cum apar în diferite aspecte sau litere alternative în monograma unei ferestre.

Cu toate acestea, în organizațiile mici, acest lucru topologie asigură actualizări rapide ale datelor.

Din moment ce faci planuri topologie, Trebuie să luați în considerare și topologie traficul de corespondență și replicări.