Valoarea critică a criteriului Fisher. Criteriul exact al lui Fisher

Testul exact al lui Fisher este un criteriu care este utilizat pentru a compara doi indicatori relativi care caracterizează frecvența unei anumite caracteristici care are două valori. Datele inițiale pentru calcularea testului exact al lui Fisher sunt de obicei grupate sub forma unui tabel cu patru câmpuri.

1. Istoricul dezvoltării criteriului

Mai întâi a fost propus criteriul Ronald Fisherîn cartea sa Design of Experiments. Acest lucru s-a întâmplat în 1935. Fischer însuși a susținut că Muriel Bristol l-a îndemnat la această idee. La începutul anilor 1920, Ronald, Muriel și William Roach erau staționați în Anglia la o stație experimentală agricolă. Muriel a susținut că poate determina ordinea în care ceaiul și laptele erau turnate în ceașcă. La acel moment, nu a fost posibil să se verifice corectitudinea declarației sale.

Acest lucru a dat naștere ideii lui Fisher despre „ipoteza nulă”. Scopul nu a fost să demonstreze că Muriel putea face diferența dintre ceștile de ceai preparate diferit. S-a decis să se infirme ipoteza că o femeie face o alegere la întâmplare. S-a stabilit că ipoteza nulă nu a putut fi nici dovedită, nici justificată. Dar poate fi respins în timpul experimentelor.

S-au pregătit 8 căni. Primele patru sunt umplute mai întâi cu lapte, celelalte patru cu ceai. Cupele au fost amestecate. Bristol s-a oferit să guste ceaiul și să împartă ceștile după metoda de preparare a ceaiului. Rezultatul ar fi trebuit să fie două grupuri. Istoria spune că experimentul a fost un succes.

Datorită testului Fisher, probabilitatea ca Bristol să acționeze intuitiv a fost redusă la 0,01428. Adică, s-a putut identifica corect cupa într-un caz din 70. Dar totuși, nu există nicio modalitate de a reduce la zero șansele pe care doamna le determină întâmplător. Chiar dacă măriți numărul de cești.

Această poveste a dat impuls dezvoltării „ipotezei nule”. În același timp, a fost propus criteriul exact al lui Fisher, a cărui esență este enumerarea tuturor combinațiilor posibile de variabile dependente și independente.

2. Pentru ce este folosit testul exact Fisher?

Testul exact al lui Fisher este folosit în principal pentru comparație mostre mici. Există două motive bune pentru aceasta. În primul rând, calcularea criteriului este destul de greoaie și poate dura mult timp sau necesită resurse de calcul puternice. În al doilea rând, criteriul este destul de precis (ceea ce se reflectă chiar și în numele său), ceea ce îi permite să fie utilizat în studii cu un număr mic de observații.

Un loc special este acordat testului exact al lui Fisher în medicină. Aceasta este o metodă importantă de prelucrare a datelor medicale și și-a găsit aplicarea în multe studii științifice. Datorită acesteia, este posibilă studierea relației dintre anumiți factori și rezultate, compararea frecvenței stărilor patologice între două grupuri de subiecți etc.

3. În ce cazuri poate fi folosit testul exact al lui Fisher?

Variabilele comparate trebuie măsurate în Scala nominalași au numai două sensuri, de exemplu, tensiunea arterială este normală sau crescută, rezultatul este favorabil sau nefavorabil, există complicații postoperatorii sau nu.
Testul exact al lui Fisher este destinat pentru comparație două grupuri independente, împărțit pe baza factorilor. În consecință, factorul ar trebui să aibă, de asemenea, doar două valori posibile.
Testul este potrivit pentru compararea probelor foarte mici: testul exact al lui Fisher poate fi utilizat pentru a analiza tabele din patru părți în cazul valorilor fenomenului așteptat mai mici de 5, ceea ce este o limitare pentru utilizarea chi-pătratului Pearson test, chiar ținând cont de corecția Yates.
Testul exact al lui Fisher poate fi unilateral și cu două fețe. Cu o opțiune unilaterală, se știe exact unde se va abate unul dintre indicatori. De exemplu, un studiu compară câți pacienți s-au recuperat în comparație cu un grup de control. Se presupune că terapia nu poate agrava starea pacienților, ci doar fie o vindecă, fie nu.
Un test cu două cozi evaluează diferențele de frecvență în două direcții. Adică, se evaluează probabilitatea unei frecvențe atât mai mari, cât și mai mici a fenomenului în grupul experimental comparativ cu grupul de control.

Un analog al testului exact al lui Fisher este testul chi-pătrat Pearson, în timp ce testul exact al lui Fisher are o putere mai mare, mai ales când se compară mostre mici și, prin urmare, are un avantaj în acest caz.

4. Cum se calculează testul exact al lui Fisher?

Să presupunem că studiem dependența frecvenței nașterilor copiilor cu malformații congenitale (CDD) de fumatul matern în timpul sarcinii. Pentru aceasta, au fost selectate două grupuri de gravide, dintre care unul a fost un grup experimental, format din 80 de femei care au fumat în primul trimestru de sarcină, iar al doilea a fost un grup de comparație, incluzând 90 de femei care duc un stil de viață sănătos pe toată durata sarcinii. Numărul cazurilor de malformații congenitale fetale determinate prin ecografie în lotul experimental a fost de 10, în lotul de comparație - 2.

Mai întâi compunem tabel de urgență cu patru câmpuri:

Testul exact al lui Fisher se calculează folosind următoarea formulă:

unde N este numărul total de subiecți din două grupuri; ! - factorial, care este produsul unui număr și a unei secvențe de numere, fiecare dintre ele mai mic decât precedentul cu 1 (de exemplu, 4! = 4 3 2 1)

Ca rezultat al calculelor, constatăm că P = 0,0137.

5. Cum se interpretează valoarea testului exact al lui Fisher?

Avantajul metodei este că criteriul rezultat corespunde valorii exacte a nivelului de semnificație p. Adică, valoarea de 0,0137 obținută în exemplul nostru este nivelul de semnificație al diferențelor dintre grupurile comparate în frecvența dezvoltării malformațiilor congenitale ale fătului. Este necesar doar să comparăm acest număr cu nivelul critic de semnificație, de obicei luat în cercetarea medicală ca fiind 0,05.

Dacă valoarea testului exact al lui Fisher este mai mare decât valoarea critică, acesta este acceptat ipoteza nulăși se concluzionează că nu există diferențe semnificative statistic în incidența rezultatului în funcție de prezența factorului de risc.
Dacă valoarea testului exact al lui Fisher este mai mică decât critică, acesta este acceptat ipoteză alternativăși se concluzionează că există diferențe semnificative statistic în incidența rezultatului în funcție de expunerea la factorul de risc.

În exemplul nostru P< 0,05, в связи с чем делаем вывод о наличии прямой взаимосвязи курения и вероятности развития ВПР плода. Частота возникновения врожденной патологии у детей курящих женщин statistic semnificativ mai mare decât nefumătorii.

Funcția FISCHER returnează transformarea Fisher a argumentelor la X . Această transformare produce o funcție care are o distribuție normală, mai degrabă decât oblică. Funcția FISCHER este utilizată pentru a testa ipoteza folosind coeficientul de corelație.

Descrierea funcției FISCHER în Excel

Când lucrați cu această funcție, trebuie să setați valoarea variabilei. Merită remarcat imediat că există unele situații în care această funcție nu va produce rezultate. Acest lucru este posibil dacă variabila:

nu este un număr. Într-o astfel de situație, funcția FISCHER va returna valoarea de eroare #VALOARE!;
are o valoare fie mai mică decât -1, fie mai mare decât 1. În acest caz, funcția FISCHER va returna valoarea de eroare #NUM!.

Ecuația care este folosită pentru a descrie matematic funcția FISCHER este:

Z"=1/2*ln(1+x)/(1-x)

Să ne uităm la utilizarea acestei funcții folosind 3 exemple specifice.

Estimarea relației dintre profit și costuri folosind funcția FISHER

Exemplul 1. Folosind datele despre activitatea organizațiilor comerciale, este necesar să se facă o evaluare a relației dintre profitul Y (milioane de ruble) și costurile X (milioane de ruble) utilizate pentru dezvoltarea produsului (prezentate în Tabelul 1).

Tabelul 1 – Date inițiale:

№	X	Y
1	210.000.000,00 RUR	95.000.000,00 RUR
2	1.068.000.000,00 RUB	76.000.000,00 RUR
3	1.005.000.000,00 RUB	78.000.000,00 RUR
4	610.000.000,00 RUR	89.000.000,00 RUR
5	768.000.000,00 RUR	77.000.000,00 RUR
6	799.000.000,00 RUR	85.000.000,00 RUR

Schema de rezolvare a unor astfel de probleme este următoarea:

Se calculează coeficientul de corelație liniară r xy;
Semnificația coeficientului de corelație liniară este verificată pe baza testului t Student. În acest caz, este înaintată și testată o ipoteză că coeficientul de corelație este egal cu zero. Statistica t este folosită pentru a testa această ipoteză. Dacă ipoteza este confirmată, statistica t are o distribuție Student. Dacă valoarea calculată t p > t cr, atunci se respinge ipoteza, ceea ce indică semnificația coeficientului de corelație liniară și deci semnificația statistică a relației dintre X și Y;
Se determină o estimare de interval pentru un coeficient de corelație liniară semnificativ statistic.
O estimare a intervalului pentru coeficientul de corelație liniară este determinată pe baza transformării z Fisher inversă;
Se calculează eroarea standard a coeficientului de corelație liniară.

Rezultatele rezolvării acestei probleme cu funcțiile utilizate în Excel sunt prezentate în Figura 1.

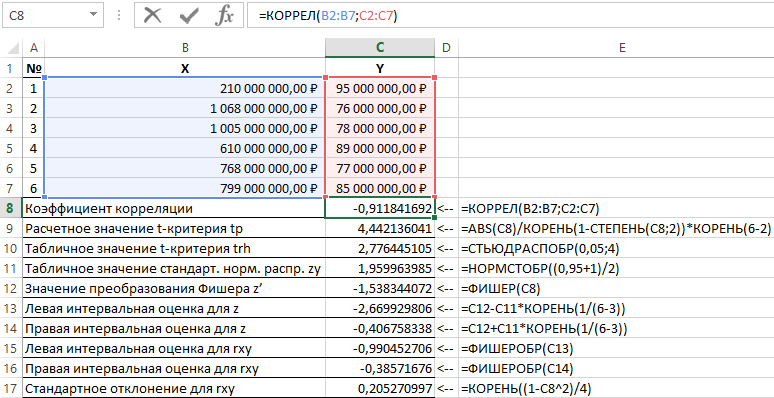
Figura 1 – Exemplu de calcule.

Nu.	Numele indicatorului	Formula de calcul
1	Coeficient de corelație	=CORREL(B2:B7;C2:C7)
2	Valoarea t-test calculată tp	=ABS(C8)/SQRT(1-PUTERE(C8,2))*SQRT(6-2)
3	Valoarea tabelului t-test trh	=STUDISCOVER(0,05,4)
4	Valoarea tabelului a distribuției normale standard zy	=NORMSINV((0,95+1)/2)
5	Valoarea transformării Fisher z’	=FISHER(C8)
6	Estimarea intervalului stâng pentru z	=C12-C11*ROOT(1/(6-3))
7	Estimarea intervalului drept pentru z	=C12+C11*ROOT(1/(6-3))
8	Estimarea intervalului stâng pentru rxy	=FISHEROBR(C13)
9	Estimarea intervalului corect pentru rxy	=FISHEROBR(C14)
10	Abaterea standard pentru rxy	=ROOT((1-C8^2)/4)

Astfel, cu o probabilitate de 0,95, coeficientul de corelație liniară se află în intervalul de la (–0,386) la (–0,990) cu o eroare standard de 0,205.

Verificarea semnificației statistice a regresiei folosind funcția FASTER

Exemplul 2. Verificați semnificația statistică a ecuației de regresie multiplă folosind testul F Fisher și trageți concluzii.

Pentru a verifica semnificația ecuației în ansamblu, propunem ipoteza H 0 despre nesemnificația statistică a coeficientului de determinare și ipoteza opusă H 1 despre semnificația statistică a coeficientului de determinare:

H1: R2≠ 0.

Să testăm ipotezele folosind testul F al lui Fisher. Indicatorii sunt prezentați în tabelul 2.

Tabelul 2 - Date inițiale

Pentru a face acest lucru, folosim funcția din Excel:

MAI RAPID (α;p;n-p-1)

α este probabilitatea asociată unei distribuții date;
p și n sunt numărătorul și, respectiv, numitorul gradelor de libertate.

Știind că α = 0,05, p = 2 și n = 53, obținem următoarea valoare pentru F crit (vezi Figura 2).

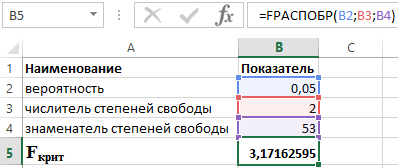
Figura 2 – Exemplu de calcule.

Astfel putem spune că F calculat > F critic. Ca urmare, este acceptată ipoteza H 1 despre semnificația statistică a coeficientului de determinare.

Calcularea valorii indicatorului de corelare în Excel

Exemplul 3. Utilizarea datelor de la 23 de întreprinderi despre: X este prețul produsului A, mii de ruble; Y este profitul unei întreprinderi comerciale, milioane de ruble sunt studiate; Modelul de regresie a fost estimat astfel: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Ce indicator de corelație poate fi determinat din aceste date? Calculați valoarea indicatorului de corelație și, folosind criteriul Fisher, trageți o concluzie despre calitatea modelului de regresie.

Să determinăm F crit din expresia:

F calculat = R 2 /23*(1-R 2)

unde R este coeficientul de determinare egal cu 0,67.

Astfel, valoarea calculată F calc = 46.

Pentru a determina F crit folosim distribuția Fisher (vezi Figura 3).

Figura 3 – Exemplu de calcule.

Astfel, estimarea rezultată a ecuației de regresie este fiabilă.

Returnează inversul distribuției de probabilitate F (coada dreaptă). Dacă p = FRIST(x;...), atunci FRIST(p;...) = x.

Distribuția F poate fi utilizată într-un test F, care compară gradul de dispersie a două seturi de date. De exemplu, puteți analiza distribuția veniturilor din Statele Unite și Canada pentru a determina dacă cele două țări sunt similare în ceea ce privește densitatea veniturilor.

Important: Această caracteristică a fost înlocuită cu una sau mai multe caracteristici noi care oferă o precizie mai mare și au nume care reflectă mai bine scopul lor. Deși această caracteristică este încă folosită pentru compatibilitate cu versiunea anterioară, este posibil să nu mai fie disponibilă în versiunile viitoare de Excel, așa că vă recomandăm să utilizați noile funcții.

Pentru a afla mai multe despre noile funcții, consultați articolele Funcția F.REV și Funcția F.REV.PH.

Sintaxă

FRIST(probabilitate,grade_libertate1,grade_libertate2)

Argumentele pentru funcția FALTER sunt descrise mai jos.

Probabilitate- argument necesar. Probabilitatea asociată cu distribuția F cumulativă.

Grade_de_libertate1- argument necesar. Numărător de grade de libertate.

Grade_de_libertate2- argument necesar. Numitorul gradelor de libertate.

Note

Dacă oricare dintre argumente nu este un număr, FRATE returnează valoarea de eroare #VALOR!

Dacă „probabilitate”< 0 или "вероятность" >1, funcția FRIST returnează valoarea de eroare #NUM!.

Dacă valoarea degrees_freedom1 sau degrees_freedom2 nu este un număr întreg, acesta este trunchiat.

Dacă „grade_libertate1”< 1 или "степени_свободы1" ≥ 10^10, функция FРАСПОБР возвращает значение ошибки #ЧИСЛО!.

Dacă „grade_libertate2”< 1 или "степени_свободы2" ≥ 10^10, функция FРАСПОБР возвращает значение ошибки #ЧИСЛО!.

Funcția FDIST poate fi utilizată pentru a determina valorile critice ale distribuției F. De exemplu, rezultatele ANOVA includ de obicei date pentru statistica F, probabilitatea F și valoarea critică a distribuției F la un nivel de semnificație de 0,05. Pentru a determina valoarea critică a lui F, trebuie să utilizați nivelul de semnificație ca argument de probabilitate al funcției FDIST.

Având în vedere o valoare de probabilitate, funcția FDIST caută o valoare a lui x pentru care FDIST(x,grade_de_libertate1,grade_de_libertate2) = probabilitate. Astfel, acuratețea funcției FDIST depinde de precizia FDIST. Pentru a căuta, funcția FRIST folosește metoda iterației. Dacă căutarea nu se termină după 100 de iterații, este returnată valoarea de eroare #N/A.

Exemplu

Copiați eșantionul de date din următorul tabel și inserați-l în celula A1 a unei noi foi de lucru Excel. Pentru a afișa rezultatele formulelor, selectați-le și apăsați F2, apoi apăsați Enter. Dacă este necesar, modificați lățimea coloanelor pentru a vedea toate datele.

Folosind acest exemplu, vom lua în considerare modul în care este evaluată fiabilitatea ecuației de regresie rezultată. Același test este folosit pentru a testa ipoteza că coeficienții de regresie sunt simultan egali cu zero, a=0, b=0. Cu alte cuvinte, esența calculelor este de a răspunde la întrebarea: poate fi folosit pentru analize și prognoze ulterioare?

Pentru a determina dacă variațiile din două eșantioane sunt similare sau diferite, utilizați acest test t.

Deci, scopul analizei este de a obține o estimare prin care să se poată afirma că la un anumit nivel de α ecuația de regresie rezultată este fiabilă statistic. Pentru aceasta se utilizează coeficientul de determinare R2.
Testarea semnificației unui model de regresie se realizează folosind testul F Fisher, a cărui valoare calculată se găsește ca raport dintre varianța seriei originale de observații a indicatorului studiat și estimarea nepărtinitoare a varianței secvenței reziduale. pentru acest model.
Dacă valoarea calculată cu k 1 =(m) și k 2 =(n-m-1) grade de libertate este mai mare decât valoarea tabelată la un anumit nivel de semnificație, atunci modelul este considerat semnificativ.

unde m este numărul de factori din model.
Semnificația statistică a regresiei liniare perechi este evaluată folosind următorul algoritm:
1. Se propune o ipoteză nulă conform căreia ecuația în ansamblu este nesemnificativă statistic: H 0: R 2 =0 la nivelul de semnificație α.
2. Apoi, determinați valoarea reală a criteriului F:

unde m=1 pentru regresia pe perechi.
3. Valoarea tabelată este determinată din tabelele de distribuție Fisher pentru un nivel de semnificație dat, ținând cont de faptul că numărul de grade de libertate pentru suma totală de pătrate (varianță mai mare) este 1 și numărul de grade de libertate pentru rezidual suma pătratelor (varianță mai mică) în regresia liniară este n-2 (sau prin funcția Excel FRIST(probabilitate,1,n-2)).
Tabelul F este valoarea maximă posibilă a criteriului sub influența unor factori aleatori cu grade date de libertate și nivelul de semnificație α. Nivelul de semnificație α este probabilitatea de a respinge ipoteza corectă, cu condiția ca aceasta să fie adevărată. De obicei, α este considerat a fi 0,05 sau 0,01.
4. Dacă valoarea reală a testului F este mai mică decât valoarea tabelului, atunci ei spun că nu există niciun motiv pentru a respinge ipoteza nulă.
În caz contrar, ipoteza nulă este respinsă și ipoteza alternativă despre semnificația statistică a ecuației în ansamblu este acceptată cu probabilitate (1-α).
Valoarea tabelului criteriului cu grade de libertate k 1 =1 și k 2 =48, F tabel = 4

concluzii: Deoarece valoarea reală F > F tabelul, coeficientul de determinare este semnificativ statistic ( estimarea ecuației de regresie găsită este fiabilă din punct de vedere statistic) .

Analiza variatiei

Indicatori de calitate a ecuației de regresie

Exemplu. Pe baza unui total de 25 de întreprinderi comerciale, se studiază relația dintre următoarele caracteristici: X - prețul produsului A, mii de ruble; Y este profitul unei întreprinderi comerciale, milioane de ruble. La evaluarea modelului de regresie s-au obţinut următoarele rezultate intermediare: ∑(y i -y x) 2 = 46000; ∑(y i -y avg) 2 = 138000. Ce indicator de corelație poate fi determinat din aceste date? Calculați valoarea acestui indicator pe baza acestui rezultat și folosind Testul F al lui Fisher trageți concluzii despre calitatea modelului de regresie.
Soluţie. Din aceste date putem determina raportul de corelație empirică: , unde ∑(y avg -y x) 2 = ∑(y i -y avg) 2 - ∑(y i -y x) 2 = 138000 - 46000 = 92.000.
η 2 = 92.000/138000 = 0,67, η = 0,816 (0,7< η < 0.9 - связь между X и Y высокая).

Testul F al lui Fisher: n = 25, m = 1.
R2 = 1 - 46000/138000 = 0,67, F = 0,67/(1-0,67)x(25 - 1 - 1) = 46. F tabel (1; 23) = 4,27
Deoarece valoarea reală F > Ftable, estimarea găsită a ecuației de regresie este fiabilă din punct de vedere statistic.

Întrebare: Ce statistici sunt folosite pentru a testa semnificația unui model de regresie?
Răspuns: Pentru semnificația întregului model în ansamblu, sunt utilizate statisticile F (testul lui Fisher).

Scop. Testarea ipotezei că două varianțe aparțin aceleiași populații generale și, prin urmare, egalitatea lor.

Ipoteza nulă. S 2 2 = S 1 2

Ipoteză alternativă. Există următoarele opțiuni pentru N A, în funcție de care diferă zonele critice:

1. S 1 2 > S 2 2 . Opțiunea cea mai frecvent utilizată este HA. Regiunea critică este coada superioară a distribuției F.

2. S 1 2< S 2 2 . Критическая область - нижний хвост F-распределения. Ввиду частого отсутствия нижнего хвоста, в таблицах критическую область обычно сводят к варианту 1, меняя местами дисперсии.

3. Face-verso S 1 2 ≠S 2 2. Combinația primelor două.

Cerințe preliminare. Datele sunt independente și distribuite normal. Ipoteza că varianțele a două populații normale sunt egale este acceptată dacă raportul dintre varianța mai mare și cea mai mică este mai mic decât valoarea critică a distribuției Fisher.

F P = S 1 2 / S 2 2

Notă. Cu metoda de verificare descrisă, valoarea lui Fpasch trebuie să fie neapărat mai mare decât unu. Criteriul este sensibil la încălcarea ipotezei de normalitate.

Pentru o alternativă cu două laturi S 1 2 ≠ S 2 2 ipoteza nulă este acceptată dacă este îndeplinită condiția:

F l - α /2< Fрасч < F α /2

Exemplu

Parametrii termofizici au fost determinați folosind o metodă termometrică complexă. caracteristicile (TFC) ale malțului verde. Pentru prepararea probelor, am luat malț uscat la aer (umiditate medie W=19%) și umed malț învechit de patru zile (W=45%) în conformitate cu noua tehnologie de preparare a malțului caramel. Experimentele au arătat că conductivitatea termică λ a malțului umed este de aproximativ 2,5 ori mai mare decât cea a malțului uscat, iar capacitatea termică volumetrică nu are o dependență clară de conținutul de umiditate al malțului. Prin urmare, folosind testul F, am verificat posibilitatea generalizării datelor pe baza valorilor medii fără a ține cont de umiditate

Datele calculate sunt rezumate în tabelul 5.1

Tabelul 5.1

Date pentru calcularea criteriului F

S-a obținut o valoare mai mare de dispersie pentru W=45%, adică. S245 = S12, S219 = S22 şi FP = S12/S22 = 1,35. Din Tabelul 5.2 pentru gradul de libertate f 1 =N 1 -1=5 f 2 =N 2 -1=4 la γ=0,95 determinăm F KR =6,2. Ipoteza nulă formulată ca „În intervalul de umiditate al malțului verde de la 19 la 45%, influența acestuia asupra capacității termice volumetrice poate fi neglijată” sau „S 2 45 = S 2 19 ” cu o probabilitate de încredere de 95% a fost confirmat, din moment ce Fp

Un exemplu de testare a unei ipoteze despre apartenența a două varianțe la aceeași populație folosind criteriul Fisher folosind Excel

Sunt prezentate date pentru două eșantioane independente (Tabelul 5.2) ale gradului de absorbție a apei a boabelor de grâu A fost efectuat un studiu al efectului câmpurilor magnetice de joasă frecvență.

Tabelul 5.2

Rezultatele cercetării

Număr	Numărul eșantionului
experienţă		2 ,
	0,027	0,075
	0,036	0,4
	0,1	0,08
	0,12	0,105
	0,32	0,075
	0,45	0,12
	0,049	0,06
	0,105	0,075

Înainte de a testa ipoteza despre egalitatea mediilor acestor eșantioane, este necesar să testăm ipoteza despre egalitatea varianțelor pentru a ști ce criteriu să alegem pentru a o testa.

În fig. 5.1 prezintă un exemplu de testare a ipotezei că două varianțe aparțin aceleiași populații folosind criteriul Fisher folosind produsul software Microsoft Excel.

Figura 5.1 Exemplu de testare a apartenenței a două varianțe la aceeași populație folosind criteriul Fisher

Datele sursă se află în celulele situate la intersecția coloanelor C și D cu rândurile 3-10. Să facem următoarele:

1. Să determinăm dacă legea de distribuție a primului și celui de-al doilea eșantion poate fi considerată normală (coloanele C și, respectiv, D). Dacă nu (cel puțin pentru o probă), atunci este necesar să folosim un test neparametric dacă da, continuăm.

2. Calculați variațiile pentru prima și a doua coloană. Pentru a face acest lucru, în celulele SP și D11 plasăm funcțiile =DISP(SZ:C10) și respectiv =DISP(DЗ:D10). Rezultatul acestor funcții este valoarea varianței calculată pentru fiecare coloană, respectiv.

3. Găsiți valoarea calculată pentru criteriul Fisher. Pentru a face acest lucru, trebuie să împărțiți varianța mai mare la cea mai mică. În celula F13 plasăm formula =C11/D11, care realizează această operație.

4. Stabiliți dacă ipoteza egalității varianțelor poate fi acceptată. Există două metode, care sunt prezentate în exemplu. Conform primei metode, prin stabilirea unui nivel de semnificație, de exemplu 0,05, se calculează valoarea critică a distribuției Fisher pentru această valoare și numărul corespunzător de grade de libertate. În celula F14, introduceți funcția =FPACPOBP(0,05;7;7) (unde 0,05 este nivelul de semnificație specificat; 7 este numărul de grade de libertate ale numărătorului și 7 (al doilea) este numărul de grade de libertate ale numitorul). Numărul de grade de libertate este egal cu numărul de experimente minus unu. Rezultatul este 3,787051. Deoarece această valoare este mai mare decât valoarea calculată de 1,81144, trebuie să acceptăm ipoteza nulă a egalității varianțelor.

Conform celei de-a doua opțiuni, probabilitatea corespunzătoare este calculată pentru valoarea calculată obținută a criteriului Fisher. Pentru a face acest lucru, introduceți funcția =FPACP(F13;7;7) în celula F15. Deoarece valoarea rezultată de 0,22566 este mai mare decât 0,05, se acceptă ipoteza egalității varianțelor.

Acest lucru se poate face printr-o funcție specială. Selectați secvențial elementele de meniu Serviciu , Analiza datelor . Va apărea următoarea fereastră (Fig. 5.2).

Figura 5.2 Fereastra de selectare a metodei de procesare

În această fereastră selectați „ F-mecm cu două mostre pentru variații " Ca rezultat, va apărea o fereastră așa cum se arată în Fig. 5.3. Aici setați intervalele (numerele de celule) ale primei și celei de-a doua variabile, nivelul de semnificație (alfa) și locul unde va fi localizat rezultatul.

Setați toți parametrii necesari și faceți clic pe OK. Rezultatul lucrării este prezentat în Fig. 5.4

Trebuie remarcat faptul că funcția testează un criteriu unilateral și o face corect. Pentru cazul în care valoarea criteriului este mai mare decât 1, se calculează valoarea critică superioară.

Figura 5.3 Fereastra de setare a parametrilor

Când valoarea criteriului este mai mică de 1, se calculează valoarea critică inferioară.

Reamintim că ipoteza egalității varianțelor este respinsă dacă valoarea criteriului este mai mare decât valoarea critică superioară sau mai mică decât cea inferioară.

Figura 5.4 Testarea egalității varianțelor