Перспективное проецирование

Нами были рассмотрены важные проекции, использующиеся в аффинной геометрии. Перейдем теперь к рассмотрению перспективной геометрии и нескольких новых видов проецирования.

На фотографиях, картинах, экране изображения кажутся нам естественными и правильными. Эти изображения называют перспективными. Свойства их таковы, что более удаленные предметы изображаются в меньших масштабах, параллельные прямые в общем случае непараллельны. В итоге геометрия изображения оказывается достаточно сложной, и по готовому изображению сложно определить размер тех или иных частей объекта.

Обычная перспективная проекция - это центральная проекция на плоскость прямыми лучами, проходящими через точку - центр проецирования. Один из проецирующих лучей перпендикулярен к плоскости проецирования и называется главным. Точка пересечения этого луча и плоскости проекции - главная точка картины.

Существует три системы координат. Обычно программист работает и держит данные о геометрических объектах в мировых координатах. Для повышения реалистичности при подготовке к выводу изображения на экран данные об объектах из мировых координат переводят в видовые координаты. И только в момент вывода изображения непосредственно на экран дисплея переходят к экранным координатам, которые представляют собой номера пикселов экрана.

Первые две системы могут использоваться в многомерных системах координат, но последняя только в двухмерной. Операции являются необратимыми, то есть из двухмерной картинки-проекции невозможно восстановить трехмерное изображение.

В этой матрице элементы a , d , е отвечают за масштабирование, m , n , L - за смещение, p , q , r - за проецирование, s - за комплексное масштабирование, х - за вращение.

Одноточечное проецирование на плоскость z = 0

Суть этого проецирования такова: чем глубже находится предмет, тем больше становится значение z-координаты и знаменателя rz + 1, и, следовательно, тем мельче выглядит предмет на плоскости проекции. Выполним несложные выкладки и поясним их графически:
уравнение x"/F = x/(F + z пр) равносильно: x" = xF/(F + z пр) = x/(1 + z пр /F) = x/(1 + rz пр), где r = 1/F, F - фокус.

Для того, чтобы точки, лежащие на линии, параллельной оси z , не терялись друг за другом, используется одноточечное проецирование на линию (см. матрицу преобразования и рис. 4.2 ); исчезла z-координата, но, поскольку дальние предметы стали более мелкими, чем такие же близкие, у зрителя появляется ощущение глубины. Запомните: это первый способ передачи глубины на плоскости!

Движок не перемещает корабль. Корабль остается на месте, а движок перемещает вселенную относительно его.

Это очень важная часть уроков, убедитесь что прочитали ее несколько раз и хорошо поняли.

Однородные координаты

До текущего момента мы оперировали 3х-мерными вершинами как (x, y, z) триплетами. Введем еще один параметр w и будем оперировать векторами вида (x, y, z, w).

Запомните навсегда, что:

• Если w == 1, то вектор (x, y, z, 1) - это позиция в пространстве.
• Если же w == 0, то вектор (x, y, z, 0) - это направление.

Что это дает нам? Ок, для поворота это ничего не меняет, так как и в случае поворота точки и в случае поворота вектора направления вы получаете один и тот же результат. Однако в случае переноса есть разница. Перенос вектора направления даст тот же самый вектор. Подробнее об этом остановимся позднее.

Однородные координаты позволяют нам с помощью одной математической формулы оперировать векторами в обоих случаях.

Матрицы трансформаций

Введение в матрицы

Проще всего представить матрицу, как массив чисел, со строго определенным количеством строк и столбцов. К примеру, матрица 2x3 выглядит так:

Однако в трехмерной графике мы будем использовать только матрицы 4x4, которые позволят нам трансформировать наши вершины (x, y, z, w). Трансформированная вершина является результатом умножения матрицы на саму вершину:

Матрица x Вершина (именно в этом порядке!!) = Трансформир. вершина

Довольно просто. Мы будем использовать это довольно часто, так что имеет смысл поручить это компьютеру:

В C++, используя GLM:

glm :: mat4 myMatrix ; glm :: vec4 myVector ; glm :: // Обратите внимание на порядок! Он важен!

В GLSL:

mat4 myMatrix ; vec4 myVector ; // Не забудьте тут заполнить матрицу и вектор необходимыми значениями vec4 transformedVector = myMatrix * myVector ; // Да, это очень похоже на GLM:)

Попробуйте поэкспериментировать с этими фрагментами.

Матрица переноса

Матрица переноса выглядит так:

где X, Y, Z - это значения, которые мы хотим добавить к нашему вектору.

Значит, если мы захотим перенести вектор (10, 10, 10, 1) на 10 юнитов в направлении X, то мы получим:

… получим (20, 10, 10, 1) однородный вектор! Не забывайте, что 1 в параметре w, означает позицию, а не направление и наша трансформация не изменила того, что мы работаем с позицией.

Теперь посмотрим, что случится, если вектор (0, 0, -1, 0) представляет собой направление:

… и получаем наш оригинальный вектор (0, 0, -1, 0). Как было сказано раньше, вектор с параметром w = 0 нельзя перенести.

И самое время перенести это в код.

В C++, с GLM:

#include // после glm :: mat4 myMatrix = glm :: translate (glm :: mat4 (), glm :: vec3 (10.0 f , 0.0 f , 0.0 f )); glm :: vec4 myVector (10.0 f , 10.0 f , 10.0 f , 0.0 f ); glm :: vec4 transformedVector = myMatrix * myVector ;

В GLSL:

vec4 transformedVector = myMatrix * myVector ;

По факту, вы никогда не будете делать это в шейдере, чаще всего вы будете выполнять glm::translate() в C++, чтобы вычислить матрицу, передать ее в GLSL, а уже в шейдере выполнить умножение

Единичная матрица

Это специальная матрица, которая не делает ничего, но мы затрагиваем ее, так как важно помнить, что A умноженное на 1.0 дает A:

В C++ :

glm :: mat4 myIdentityMatrix = glm :: mat4 (1.0 f );

Матрица масштабирования

Выглядит также просто:

Значит, если вы хотите применить масштабирование вектора (позицию или направление - это не важно) на 2.0 во всех направлениях, то вам необходимо:

Обратите внимание, что w не меняется, а также обратите внимание на то, что единичная матрица - это частный случай матрицы масштабирования с коэффициентом масштаба равным 1 по всем осям. Также единичная матрица - это частный случай матрицы переноса, где (X, Y, Z) = (0, 0, 0) соответственно.

В C++ :

// добавьте #include и #include glm :: mat4 myScalingMatrix = glm :: scale (2.0 f , 2.0 f , 2.0 f );

Матрица поворота

Сложнее чем рассмотренные ранее. Мы опустим здесь детали, так как вам не обязательно знать это точно для ежедневного использования. Для получения более подробной информации можете перейти по ссылке Matrices and Quaternions FAQ (довольно популярный ресурс и возможно там доступен ваш язык)

В C++ :

// добавьте #include и #include glm :: vec3 myRotationAxis ( ?? , ?? , ?? ); glm :: rotate ( angle_in_degrees , myRotationAxis );

Собираем трансформации вместе

Итак, теперь мы умеем поворачивать, переносить и масштабировать наши векторы. Следующий шагом было бы неплохо объединить трансформации, что реализуется по следующей формуле:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector ;

ВНИМАНИЕ! Эта формула на самом деле показывает, что сначала выполняется масштабирование, потом поворот и только в самую последнюю очередь выполняется перенос. Именно так работает перемножение матриц.

Обязательно запомните в каком порядке все это выполняется, потому что порядок действительно важен, в конце концов вы можете сами это проверить:

• Сделайте шаг вперед и повернитесь влево
• Повернитесь влево и сделайте шаг вперед

Разницу действительно важно понимать, так как вы постоянно будете с этим сталкиваться. К примеру, когда вы будете работать с игровыми персонажами или какими-то объектами, то всегда сначала выполняйте масштабирование, потом поворот и только потом перенос.

На самом деле, приведенный выше порядок - это то, что вам обычно нужно для игровых персонажей и других предметов: сначала масштабируйте его, если это необходимо; затем установливаете его направление, а затем перемещаете его. Например, для модели судна (повороты удалены для упрощения):

• Неправильный путь:
  • Вы переносите корабль на (10, 0, 0). Его центр теперь находится в 10 единицах от начала координат.
  • Вы масштабируете свой корабль в 2 раза. Каждая координата умножается на 2 “относительно исходной”, что далеко… Итак, вы попадаете в большой корабль, но его центр 2 * 10 = 20. Не то, что вы хотели.
• Правильный путь:
  • Вы масштабируете свой корабль в 2 раза. Вы получаете большой корабль, с центром в начале координат.
  • Вы переносите свой корабль. Он по прежнему того же размера и на правильном расстоянии.

В C++, с GLM:

glm :: mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix ; glm :: vec4 myTransformedVector = myModelMatrix * myOriginalVector ;

В GLSL:

mat4 transform = mat2 * mat1 ; vec4 out_vec = transform * in_vec ;

Мировая, видовая и проекционная матрицы

До конца этого урока мы будем полагать, что знаем как отображать любимую 3D модель из Blender - обезьянку Suzanne.

Мировая, видовая и проекционная матрицы - это удобный инструмент для разделения трансформаций.

Мировая матрица

Эта модель, также, как и наш красный треугольник задается множеством вершин, координаты которых заданы относительно центра объекта, т. е. вершина с координатами (0, 0, 0) будет находиться в центре объекта.

Далее мы бы хотели перемещать нашу модель, так как игрок управляет ей с помощью клавиатуры и мышки. Все, что мы делаем - это применяем масштабирование, потом поворот и перенос. Эти действия выполняются для каждой вершины, в каждом кадре (выполняются в GLSL, а не в C++!) и тем самым наша модель перемещается на экране.

Теперь наши вершины в мировом пространстве. Это показывает черная стрелка на рисунке. Мы перешли из пространства объекта (все вершины заданы относительно центра объекта) к мировому пространству (все вершины заданы относительно центра мира).

Схематично это показывается так:

Видовая матрица

Еще раз процитируем Футураму:

Движок не перемещает корабль. Корабль остается на том же месте, а движок перемещает вселенную вокруг него.

Попробуйте представить это применительно к камере. Например, если вы хотите сфотографировать гору, то вы не перемещаете камеру, а перемещаете гору. Это не возможно в реальной жизни, но это невероятно просто в компьютерной графике.

Итак, изначально ваша камера находится в центре мировой системы координат. Чтобы переместить мир вам необходимо ввести еще одну матрицу. Допустим, что вы хотите переместить камеру на 3 юнита ВПРАВО (+X), что будет эквивалентом перемещения всего мира на 3 юнита ВЛЕВО (-X). В коде это выглядит так:

// Добавьте #include и #include glm :: mat4 ViewMatrix = glm :: translate (glm :: mat4 (), glm :: vec3 (- 3.0 f , 0.0 f , 0.0 f ));

Опять же, изображение ниже полностью показывает это. Мы перешли из мировой системы координат (все вершины заданы относительно центра мировой системы) к системе координат камеры (все вершины заданы относительно камеры):

И пока ваш мозг переваривает это, мы посмотрим на функцию, которую предоставляет нам GLM, а точнее на glm::LookAt:

glm :: mat4 CameraMatrix = glm :: LookAt ( cameraPosition , // Позиция камеры в мировом пространстве cameraTarget , // Указывает куда вы смотрите в мировом пространстве upVector // Вектор, указывающий направление вверх. Обычно (0, 1, 0) );

А вот диаграмма, которая показывает то, что мы делаем:

Однако это еще не конец.

Проекционная матрица

Итак, теперь мы находимся в пространстве камеры. Это означает, что вершина, которая получит координаты x == 0 и y == 0 будет отображаться по центру экрана. Однако, при отображении объекта огромную роль играет также дистанция до камеры (z). Для двух вершин, с одинаковыми x и y, вершина имеющая большее значение по z будет отображаться ближе, чем другая.

Это называется перспективной проекцией:

И к счастью для нас, матрица 4х4 может выполнить эту проекцию :

// Создает действительно трудночитаемую матрицу, но, тем не менее это стандартная матрица 4x4 glm :: mat4 projectionMatrix = glm :: perspective ( glm :: radians (FoV ), // Вертикальное поле зрения в радианах. Обычно между 90° (очень широкое) и 30° (узкое) 4.0 f / 3.0 f , // Отношение сторон. Зависит от размеров вашего окна. Заметьте, что 4/3 == 800/600 == 1280/960 0.1 f , // Ближняя плоскость отсечения. Должна быть больше 0. 100.0 f // Дальняя плоскость отсечения. );

Мы перешли из Пространства Камеры (все вершины заданы относительно камеры) в Однородное пространство (все вершины находятся в небольшом кубе. Все, что находится внутри куба - выводится на экран).

Теперь посмотрим на следующие изображения, чтобы вы могли лучше понять что же происходит с проекцией. До проецирования мы имеем синие объекты в пространстве камеры, в то время как красная фигура показывает обзор камеры, т. е. все то, что видит камера.

Применение Проекционной матрицы дает следующий эффект:

На этом изображении обзор камеры представляет собой куб и все объекты деформируются. Объекты, которые находятся ближе к камере отображаются большими, а те, которые дальше - маленькими. Прямо как в реальности!

Вот так это будет выглядеть:

Изображение является квадратным, поэтому следующие математические трансформации применяются, чтобы растянуть изображение согласно актуальным размерам окна:

И это изображение является тем, что на самом деле будет выведено.

Объединяем трансформации: матрица ModelViewProjection

… Просто стандартные матричные преобразования, которые вы уже полюбили!

// C++ : вычисление матрицы glm :: mat4 MVPmatrix = projection * view * model ; // Запомните! В обратном порядке!

// GLSL: применение матрицы transformed_vertex = MVP * in_vertex ;

Совмещаем все вместе

• Первый шаг - создание нашей MVP матрицы. Это должно быть сделано для каждой модели, которую вы отображаете.

// Проекционная матрица: 45° поле обзора, 4:3 соотношение сторон, диапазон: 0.1 юнит <-> 100 юнитов glm :: mat4 Projection = glm :: perspective (glm :: radians (45.0 f ), 4.0 f / 3.0 f , 0.1 f , 100.0 f ); // Или, для ортокамеры glm :: mat4 View = glm :: lookAt ( glm :: vec3 (4 , 3 , 3 ), // Камера находится в мировых координатах (4,3,3) glm :: vec3 (0 , 0 , 0 ), // И направлена в начало координат glm :: vec3 (0 , 1 , 0 ) // "Голова" находится сверху ); // Матрица модели: единичная матрица (Модель находится в начале координат) glm :: mat4 Model = glm :: mat4 (1.0 f ); // Индивидуально для каждой модели // Итоговая матрица ModelViewProjection, которая является результатом перемножения наших трех матриц glm :: mat4 MVP = Projection * View * Model ; // Помните, что умножение матрицы производиться в обратном порядке

• Второй шаг - передать это в GLSL:

// Получить хэндл переменной в шейдере // Только один раз во время инициализации. GLuint MatrixID = glGetUniformLocation (programID , "MVP" ); // Передать наши трансформации в текущий шейдер // Это делается в основном цикле, поскольку каждая модель будет иметь другую MVP-матрицу (как минимум часть M) glUniformMatrix4fv (MatrixID , 1 , GL_FALSE , & MVP [ 0 ][ 0 ]);

• Третий шаг - используем полученные данные в GLSL, чтобы трансформировать наши вершины.

// Входные данные вершин, разные для всех исполнений этого шейдера. layout (location = 0 ) in vec3 vertexPosition_modelspace ; // Значения, которые остаются постоянными для всей сетки. uniform mat4 MVP ; void main (){ // Выходная позиция нашей вершины: MVP * position gl_Position = MVP * vec4 (vertexPosition_modelspace , 1 ); }

• Готово! Теперь у нас есть такой же треугольник как и в Уроке 2, все так же находящийся в начале координат (0, 0, 0), но теперь мы его видим в перспективе из точки (4, 3, 3).

В Уроке 6 вы научитесь изменять эти значения динамически, используя клавиатуру и мышь, чтобы создать камеру, которую вы привыкли видеть в играх. Но для начала мы узнаем как придать нашем моделям цвета (Урок 4) и текстуры (Урок 5).

Задания

• Попробуйте поменять значения glm::perspective
• Вместо использования перспективной проекции попробуйте использовать ортогональную (glm:ortho)
• Измените ModelMatrix для перемещения, поворота и масштабирования треугольника
• Используйте предыдущее задание, но с разным порядком операций. Обратите внимание на результат.

Аксонометрия является параллельной проекцией. В табл.3.3 первыми приводятся матрицы ортографических проекций на координатные плоскости, полученные из их определений.

Табл.3.3.Матрицы проектирующих преобразований и проецирования

Ортографическая проекция на XOY		Ортографическая проекция на YOZ
Ортографическая проекция на XOZ		Ортографическая проекция на плоскость x=p
Матрица триметрического преобразования на плоскость XOY
Матрица изометрического преобразования на плоскость XOY
Матрица изометрического проецирования на плоскость XOY
Матрица косоугольной проекции на XOY	Матрица свободной проекции на XOY
Матрица кабинетной проекции на XOY	Матрица перспективного преобразования с одной точкой схода (картинная плоскость перпендикулярна оси абсцисс)
Матрица перспективного преобразования с одной точкой схода (картинная плоскость перпендикулярна оси ординат)		Матрица перспективного преобразования с одной точкой схода (картинная плоскость перпендикулярна оси аппликат)
Матрица перспективного преобразования с двумя точками схода (картинная плоскость параллельна оси ординат)		Матрица перспективного преобразования с тремя точками схода (картинная плоскость произвольного положения)

Изометрия, диметрия и триметрия получаются комбинацией поворотов, за которыми следует проекция из бесконечности. Если нужно описать проекцию на плоскость XOY, то сначала необходимо осуществить преобразование поворота на угол относительно оси ординат, затем на уголотносительно оси абсцисс. В табл.3.3 приведена матрица триметрического преобразования. Для получения матрицы диметрического преобразования, при котором, например, коэффициенты искажения по осям абсцисс и ординат будут равными, взаимосвязь между углами поворотов должна подчиняться зависимости

То есть, выбрав угол , можно вычислить уголи определить матрицу диметрической проекции. Для изометрического преобразования взаимосвязь этих углов превращается в строго определенные значения, составляющие:

В табл.3.3 приведена матрица изометрического преобразования, а также матрица изометрического проецирования на плоскость XOY. Необходимость в матрицах первого типа заключается в их использовании в алгоритмах удаления невидимых элементов.

В косоугольных проекциях проектирующие прямые образуют с плоскостью проекции угол, отличный от 90 градусов. В табл.3.3 приведена общая матрица косоугольной проекции на плоскость XOY, а также матрицы свободной и кабинетной проекций, в которых:

Перспективные проекции (табл.3.3) также представлены перспективными преобразованиями и перспективными проекциями на плоскость XOY. V X , V Y и V Z являются центрами проецирования - точками на соответствующих осях. –V X , -V Y , -V Z будут точками, в которых сходятся пучки прямых, параллельных соответствующим осям.

Система координат наблюдателя представляет собой левую систему координат (рис.3.3), в которой ось z e направлена из точки зрения вперед, ось x e направлена вправо, а ось y e – вверх. Такое правило принято для совпадения осей x e и y e с осями x s и y s на экране. Определение значений координат экрана x s и y s для точки Р приводит к необходимости деления на координату z e . Для построения точного перспективного образа необходимо выполнять деление на координату глубины каждой точки.

В табл.3.4 приведены значения дескриптора вершин S(X,Y,Z) модели (рис.2.1), подвергнутой преобразованиям поворотов и изометрическому преобразованию.

Табл.3.4.Дескрипторы вершин модели

Исходная модель				M(R(z,90))xM(R(y,90))

Для детального описания методов отслеживания точечных особенностей, калибровки камеры и реконструкции трехмерных объектов необходимо ввести модель перспективной проектирования и описать геометрические свойства этого преобразования. Точки нескольких изображений, полученных с помощью перспективной проекции, находятся в особых отношениях друг с другом, которые описываются эпиполярной геометрией. Модели этих отношений должны быть подробно рассмотрены, т.к. практически все методы трехмерной реконструкции требуют оценки соответствующих моделей и опираются на их свойства.

Необходимо отметить отдельно предположение, что на всех исходных изображениях запечатлена одна и та же сцена, т.е. каждое изображение является видом сцены с какой-то определенной камеры. Поэтому для удобства описания вводится понятие вида, как изображение с ассоциированной с ним моделью камеры, с которой оно было получено.

Перспективная проекция

Модель перспективной проекции соответствует идеальной камере-обскуре. Эта модель довольно точно соответствует процессу построения изображения в большинстве современных фото- и видеокамер. Однако из-за ограничений современной оптики реальный процесс несколько отличается от модели камеры-обскуры. Отличия реального процесса от модели называются искажениями и моделируются отдельно.

Модель простейшей камеры-обскуры удобна тем, что она полностью описывается центром проекции и положением плоскости изображения. Поэтому проекция любой точки сцены на изображении может быть найдена как пересечение луча, соединяющего центр проекции и точку сцены, с плоскостью изображения.

Простейшая модель перспективной проекции

Рассмотрим простейший случай, когда центр проекции камеры (фокус) помещен в начало системы координат, и плоскость изображения совпадает с плоскостью Z=1. Пусть (X,Y,Z) - координаты точки в 3-х мерном пространстве, а (x,y) - проекция этой точки на изображение I. Перспективная проекция в этом случае описывается следующими уравнениями:

В матричной форме с использованием однородных координат эти уравнения переписываются в следующем виде:

(2.2)

Плоскость, расположенная на расстоянии 1 от центра проекции, и перпендикулярная оптической оси называется идеальной плоскостью изображения. Оптическая ось пересекает идеальную плоскость изображения в точке с, называемой принципиальной точкой. Иллюстрация простейшего случая перспективной проекции приведена на рис. 1.

Внутренняя калибровка камеры

Простейший случай перспективной проекции практически всегда не соответствует реальной камере. Расстояние от центра проекции до плоскости изображения, т.е. фокусное расстояние, обозначаемое f, обычно не равно 1. Также координаты точки в плоскости изображения могут не совпадать с абсолютными координатами. При использовании цифровой камеры, соотношение между координатами точки в изображении и абсолютными координатами точки на идеальной плоскости, определяется формой и размерами пикселов матрицы.

Обозначим размеры пиксела матрицы цифровой камеры за p x , p y , угол наклона пиксела за α, а принципиальную точку за , рис.2. Тогда координаты точки (x,y) в изображении, соответствующей точке (x R , y R) на идеальной плоскости, определяются выражением:

(2.3)

Если за f x ,f y обозначить фокусное расстояние f, измеренное в ширинах и высотах пикселей, а tan(α)*f/p y обозначить как s, то формула 2.3 преобразуется в:

(2.4)

Матрица K называется матрицей внутренней калибровки камеры. В большинстве случаев у реальных цифровых камер угол наклона пикселей близок к прямому, т.е. параметр s=0, а ширина и высота пикселя равны. Принципиальная точка обычно располагается в центре изображения. Поэтому матрица K может быть записана в виде:

(2.5)

Это предположение о виде матрицы K широко используются для упрощения алгоритмов определения внутренней калибровки камеры, а также при синтетическом моделировании изображений, необходимых для оценки качества и эффективности методов трехмерной реконструкции.

Внешняя калибровка камеры

Пусть M - точка сцены в 3-х мерном пространстве. Любое движение является евклидовым преобразованием пространства, поэтому в однородных координатах оно выражается как:

(2.6)

где R - матрица вращения, T= T - вектор переноса.

Движение камеры относительно сцены эквивалентно обратному движению точек сцены относительно камеры, поэтому равно:

(2.7)

где R, T - матрица вращения и вектор перемещения камеры относительно сцены. Матрица С называется матрицей внешней калибровки камеры. Матрица C -1 называется матрицей движения камеры . Таким образом, матрица внешней калибровки камеры переводит координаты точек сцены из системы координат сцены в систему координат, связанную с камерой.

Полная модель перспективной проекции

Из выражений 2.1, 2.4, 2.7 можно вывести выражение произвольной перспективной проекции для любой камеры с произвольной ориентацией и положением в пространстве:

В более краткой форме с учетом предыдущих обозначений эта формула может быть записана как:

Матрица P называется матрицей проекции камеры.

По аналогии с общим перспективным преобразованием рассмотрим вначале простейший случай перспективного преобразования плоскости. Пусть плоскость p совпадает с плоскостью Z=0, тогда однородные трехмерные координаты любой ее точки M=. Для любой камеры с матрицей проекции P, перспективное преобразование плоскости описывается матрицей размерности 3*3:

Поскольку любую плоскость в 3-х мерном пространстве можно перевести в плоскость Z = 0 евклидовым преобразованием поворота и переноса, что эквивалентно домножению матрицы камеры P на матрицу преобразования L, то перспективное отображение произвольной плоскости в пространстве описывается линейным преобразованием с матрицей размерности 3*3.

Перспективное преобразование плоскости также называется гомографией . В матричной форме перспективное преобразование плоскости записывается как m=HM .

Геометрия двух изображений

Запечатленная на всех исходных изображениях сцена считается неподвижной, поэтому взаимное расположение проекций точек сцены на разных кадрах не может меняться произвольным образом. Ограничения, накладываемые на расположение проекций точек, очевидно зависят от параметров камер и их положения друг относительно друга. Поэтому определение моделей таких ограничений дает часть информации о взаимном расположении камер, с которых были получены изображения.

Перспективное преобразование плоскости

Если центры двух камер совпадают, то точки на плоскостях изображения обеих камер переводятся друг в друга перспективным преобразованием плоскости. В этом случае, преобразование точек между изображениями не зависит от формы 3-х мерной сцены, а зависит только от взаимного положения плоскостей изображений.

Если вся сцена или ее часть представляет собой плоскость, то ее изображения на разных видах с несовпадающими центрами камер, можно перевести друг в друга преобразованием гомографии. Пусть p - наблюдаемая плоскость, H 1 - преобразование гомографии между плоскостью p и изображением I 1 , H 2 - преобразование гомографии между плоскостью p и изображением I 2 . Тогда преобразование гомографии H 12 между изображениями I 1 и I 2 можно вывести следующим образом:

H 12 не зависит от параметризации плоскости p, а значит не зависит и от системы координаты в пространстве

Большинство методов определения координат 3х мерных точек по их проекциям и методов реконструкции 3-х мерной сцены, опираются на предположение о движении центра камеры между видами. Поэтому при совпадении центров камер нескольких видов эти методы будут давать некорректные результаты. Такие конфигурации камер должны обнаруживаться и обрабатываться специальным образом.

Поскольку преобразование гомографии записано в однородных координатах, то матрица H определена с точностью до масштаба. Она имеет 8 степеней свободы, и параметризируется 8 переменными. Каждое известная пара соответствующих точек m 1 и m 2 на первом и втором изображении соответственно дает 2 линейных уравнения от элементов матрицы H. Поэтому 4-х известных пар соответствующих точек достаточно для составления системы линейных уравнений из 8 уравнений с 8 неизвестными. По этой системе гомография H может быть однозначно определена, если никакие три из точек не лежат на одной прямой.

Фундаментальная матрица

Рассмотрим случай, когда центры камер двух видов не совпадают. Пусть C 1 и C 2 - центры двух камер, M - 3-х мерная точка сцены, m 1 и m 2 - проекции точки M на первое и второе изображение соответственно. Пусть П - плоскость, проходящая через точку M и центры камер C 1 и C 2 . Плоскость П пересекает плоскости изображений первого и второго видан по прямым l 1 и l 2 . Поскольку лучи C 1 M и C 2 M лежат в плоскости П, то очевидно, что точки m 1 и m 2 лежат на прямых l 1 и l 2 соответственно. Можно дать более общее утверждение, что проекции любой точки M", лежащей в плоскости П, на оба изображения должны лежать на прямых l 1 и l 2 . Эти прямые называются эпиполярными линиями. Плоскость П называются эпиполярной плоскостью.

Два вида одной и той же сцены называются стереопарой, а отрезок C 1 C 2 , соединяющий центры камер, называется базой стереопары (baseline) или стереобазой. Любая эпиполярная плоскость проходит через отрезок C 1 C 2 . Пусть C 1 C 2 пересекает первое и второе изображение в точках e 1 и e 2 соответственно. Точки e 1 и e 2 называются эпиполярными точками или эпиполями. Все эпиполярные линии пересекаются в точках e 1 и e 2 на первом и втором изображении соответственно. Множество эпиполярных плоскостей представляет собой пучок, пересекающийся по стереобазе C 1 C 2 . Множество эпиполярных линий на обоих изображений также представляют собой пучки прямых, пересекающихся в e 1 и e 2 .

Точки m 1 и m 2 называются соответствующими, если они являются проекциями одной и той же точки сцены M. Эпиполярные линии l 1 и l 2 называются соответствующими, если они лежат в одной и той же эпиполярной плоскости П. Если эпиполярная плоскость П проходит через точку m 1 , тогда эпиполярные линии l 1 и l 2 , лежащие в ней, называются соответствующими точке m 1 .

Ограничение на положение соответствующих точек m 1 и m 2 , вытекающей из эпиполярной геометрии, можно сформулировать следующим образом: точка m 2 , соответствующая m 1 , должна лежать на эпиполярной линии l 2 , соответствующей m 1 . Это условие называется эпиполярным ограничением. В однородных координатах условие того, что точка m лежит на линии l записывается как l T m=0 . Эпиполярная линия проходит также через эпиполярную точку. Уравнение прямой, проходящей через точки m 1 и e 1 можно записать как:

l 1 ∼ x m 1 ,

где x - антисимметричная матрица размерности 3*3 такая что, x m 1 - векторное произведение m 1 и e 1 .

Для соответствующих эпиполярные линий l 1 и l 2 верно:

где P + - псевдоинверсия матрицы P.

Матрица F называется фундаментальной матрицей. Она представляет собой линейный оператор, сопоставляющей каждой точке m 1 соответствующую ей эпиполярную линию l 2 . Для каждой пары соответствующих точек m 1 и m 2 верно

m T 2 Fm 1 =0

Это формулировка эпиполярного ограничения через фундаментальную матрицу.

Фундаментальная матрица имеет 7 степеней свободы. Каждая пара соответствующих точек m 1 и m 2 задает одно линейное уравнение на элементы матрицы, поэтому она может быть вычислена по известным 7 парам соответствующих точек.

Эпиполярное ограничение справедливо для любых пар соответствующих точек, расположенных на идеальных плоскостях двух видов. Если известны матрицы внутренней калибровки K 1 и K 2 камер обоих видов, то эпиполярное ограничение для соответствующих точек на идеальных плоскостях записывается как:

Матрица E называется существенной матрицей. Можно показать, что существенная матрица также может быть получена из взаимного расположения камер.

Пусть P 1 =(I|0) и P 2 =(R|-RT) - две матрицы проектирования с калибровкой K = I. Тогда уравнения проектирования на идеальную плоскость обеих камер записываются в виде:

Найдем эпиполярную линию на втором виде, соответствующую точке m" 1 на первом. Для этого достаточно спроектировать на второй вид две точки, лежащие на луче (C 1 ,m" 1) на второй вид, например центр первой камеры (0,0,0,1) T и точку на плоскости бесконечности (x" 1 ,y" 1 ,z" 1 ,0) T . Проекциями этих точек будут являться соответственно -RT, и R(x" 1 ,y" 1 ,z" 1 ,0) T . Уравнение эпиполярной линии l 2 , проходящей через обе этих точки задается как векторное произведение:

l 2 =RT×R(x" 1 ,y" 1 ,z" 1) T =R(T×(x" 1 ,y" 1 ,z" 1) T)

В матричной форме векторне произведение T×(x" 1 ,y" 1 ,z" 1) T можно записать с помощью матрицы S:

Тогда эпиполярное ограничение на точки в идеальной плоскости записывается как:

Выражение существенной матрицы через параметры внешней калибровки двух камер используется для вычисления относительного положения камер.

Геометрические свойства трех и более изображений

Пусть C 1 ,C 2 и C 3 - центры трех видов одной и той же трехмерной сцены. В этом случае, эпиполярные ограничения накладываются на соответствующие точки любой пары видов. Если известны проекции двух точек m 1 и m 2 на первый и второй вид, то положение проекции на третье изображение может быть найдено как пересечение двух эпиполярных видов, соответствующих точкам m 1 и m 2 .

По двум известным проекциям m 1 и m 2 на два изображения с известной калибровкой можно определить положение точки M в пространстве. Поэтому если известна калибровка третьего изображения, то проекция точки M на третий вид может быть определена простой проекцией.

Ограничения, накладываемые на положение соответствующих точек более двух изображений, также можно записать в линейной форме. Для трех видов эти ограничения записываются в виде трифокального тензора, для четырех видов - в форме квадрифокального тензора. Однако вычисление этих ограничений эквивалентно вычислению калибровки всех трех или четырех видов в проективном пространстве. В этой работе эти виды ограничений не используются, поэтому более подробно не рассматриваются.

Двигатель не двигает корабль.
Корабль остается на месте, а
двигатели двигают вселенную
вокруг него.

Футурама

Это один из самых важных уроков. Вдумчиво прочитайте его хотя бы восемь раз.

Гомогенные координаты

В предыдущих уроках мы предполагали, что вершина расположена по координатам (x, y, z). Давайте-ка добавим еще одну координату – w. Отныне вершины у нас будут по координатам (x, y, z, w)

Вскоре вы поймете, что к чему, но пока примите это как данность:

• Если w==1, тогда вектор (x,y,z,1) – это позиция в пространстве
• Если w==0, тогда вектор (x,y,z,0) – это направление.

Запомните это как аксиому без доказательств!!!

И что это нам дает? Ну, для вращения ничего. Если вы вращаете точку или направление, то получите один и тот же результат. Но если вы вращаете перемещение(когда вы двигаете точку в определенном направлении), то все кардинально меняется. А что значит «переместить направление»? Ничего особенного.

Гомогенные координаты позволяют нам оперировать единым матаппаратом для обоих случаев.

Матрицы Трансформаций

Введение в матрицы

Если по простому, то матрица, это просто массив чисел с фиксированным количеством строк и столбцов.

Например, матрица 2 на 3 будет выглядеть так:

В 3д графике мы пользуемся почти всегда матрицами 4х4. Это позволяет нам трансформировать наши (x,y,z,w) вершины. Это очень просто – мы умножаем вектор позиции на матрицу трансформации.

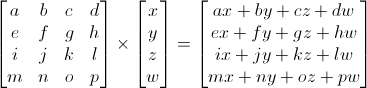
Матрица*Вершину = трансформированная вершина

Все не так страшно как выглядит. Укажите пальцем левой руки на a, а пальцем правой руки на x. Это будет ax. Переместите левый палец на следующее число b, а правый палец вниз на следующее число – y. У нас получилось by. Еще раз – cz. И еще раз – dw. Теперь суммируем все получившиеся числа – ax+by +cz +dw . Мы получили наш новый x. Повторите то же самое для каждой строки и вы получите новый вектор (x,y,z,w).

Однако это довольно скучная операция, так что пусть её за нас будет выполнять компьютер.

В С++ при помощи библиотеки GLM:

glm::mat4 myMatrix;

glm::vec4 myVector;

glm :: vec 4 transformedVector = myMatrix * myVector ; // Не забываем про порядок!!! Это архиважно!!!

В GLSL:

mat4 myMatrix;

vec4 myVector;

// заполняем матрицу и вектор нашими значениями… это мы пропускаем

vec 4 transformedVector = myMatrix * myVector ; // точно так же как и в GLM

(Чего-то мне кажется, что вы не скопировали этот кусок кода к себе в проект и не попробовали…ну же, попробуйте, это интересно!)

Матрица перемещений

Матрица перемещения, это, наверное, самая простая матрица из всех. Вот она:

Тут X, Y, Z – это значения, которые мы хотим добавить к нашей позиции вершины.

Итак, если нам нужно переместить вектор (10,10,10,1) на 10 пунктов, по позиции Х, то:
(Попробуйте это сами, ну пожаааалуйста!)

…И у нас получится (20,10,10,1) в гомогенном векторе. Как вы, я надеюсь, помните, 1 значит, что вектор представляет собой позицию, а не направление.

А теперь давайте попробуем таким же образом трансформировать направление (0,0,-1,0):

И в итоге у нас получился тот же вектор (0,0,-1,0).
Как я и говорил, двигать направление не имеет смысла.

Как же нам закодить это?

В С++ при помощи GLM:

#include // после

glm::mat4 myMatrix = glm::translate(10.0f, 0.0f, 0.0f );

glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f );

glm :: vec 4 transformedVector = myMatrix * myVector ; // и какой у нас получится результат?

А в GLSL: В GLSL так редко кто делает. Чаще всего с помощью функции glm::translate(). Сначала создают матрицу в С++, а затем отправляют её в GLSL, и уже там делают лишь одно умножение:

vec4 transformedVector = myMatrix * myVector;

Единичная матрица(Identity Matrix)

Это специальная матрица. Она не делает ничего. Но я упоминаю её, так как важно знать, что умножение A на 1.0 в результате дает А:

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

Матрица Масштабирования

Матрица масштабирования так же достаточно проста:

Поэтому если вам хочется увеличить вектор(позицию или направление, не важно) в два раза по всем направлениям:

А координата w не поменялась. Если вы спросите: «А что такое масштабирование направления?». Полезно не часто, но иногда полезно.

(заметьте, что масштабирование единичной матрицы с (x,y,z) = (1,1,1))

С++:

// Используйте #include и #include

glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

Матрица Вращения

А вот эта матрица достаточно сложная. Поэтому я не буду останавливаться на подробностях её внутренней реализации. Если сильно хочется, лучше почитайте (Matrices and Quaternions FAQ)

В С ++:

// Используйте #include и #include

glm::vec3 myRotationAxis(??, ??, ??);

glm::rotate(angle_in_degrees, myRotationAxis);

Совмещенные Трансформации

Теперь мы знаем как вращать, перемещать и масштабировать наши вектора. Хорошо бы узнать, как объединить все это. Это делается просто умножением матриц друг на друга.

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

И снова порядок!!! Сначала нужно изменить размер, потом прокрутить и лишь потом сдвинуть.

Если мы будем применять трансформации в другом порядке, то не получим такой же результат. Вот попробуйте:

• Сделайте шаг вперед(не свалите компьютер со стола) и повернитесь влево
• Повернитесь влево и сделайте один шаг вперед.

Да, нужно всегда помнить про порядок действий при управлении, например, игровым персонажем. Сначала, если нужно, делаем масштабирование, потом выставьте направление(вращение) а потом перемещайте. Давайте разберем небольшой пример(я убрал вращение для облегчения расчетов):

Не правильный способ:

• Перемещаем корабль на (10,0,0). Его центр теперь на 10 по Х от центра.
• Увеличиваем размер нашего корабля в 2 раза. Каждая координата умножается на 2 относительно центра который далеко… И в итоге у нас получается корабль необходимого размера но по позиции 2*10=20. Что не совсем то, чего мы хотели.

Правильный способ:

• Увеличиваем размер корабля в 2 раза. Теперь у нас есть большой корабль расположенный по центру.
• Перемещаем корабль. Размер корабля не изменился и он расположен в нужном месте.

Умножение матрицы на матрицу выполняется почти так же, как и умножение матрицы на вектор. Не будем вдаваться в подробности, а любопытствующие пусть почитают это из специализированных источников. Мы же просто будем полагаться на библиотеку GLM.
ВС++:
glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;
В GLSL:
mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

Матрицы Модели, Вида и Проекции

Для иллюстраций предполагаем, что мы уже умеем рисовать в OpenGL любимую 3д модель программы Blender – голову обезьяны Сюзанны.

Матрицы Модели, Вида и Проекции очень удобный метод разделения трансформаций. Если сильно хочется, вы можете не использовать их(мы же не использовали их в уроках 1 и 2). Но я настойчиво рекомендую вам пользоваться ими. Просто почти все 3д библиотеки, игры итд используют их для разделения трансформаций.

Матрица Модели

Данная модель, как и наш любимый треугольничек, задана набором вершин. X, Y, Z координаты заданы относительно центра объекта. Так вот, если вершина расположена по координатам (0,0,0), то она находится в центре всего объекта

Теперь мы имеем возможность двигать нашу модель. Например, потому, что пользователь управляет ей с помощью клавиатуры и мыши. Это сделать очень просто: масштабирование*вращение*перемещение и все. Вы применяете вашу матрицу ко всем вершинам в каждом кадре(в GLSL а не в C++) и все перемещается. Все что не перемещается – расположено в центре «мира».

Вершины находятся в мировом пространстве Черная стрелка на рисунке показывает, как мы переходим из пространства модели, в мировое пространство(Все вершины были заданы относительно центра модели, а стали заданы относительно центра мира)

Эту трансформацию можно отобразить следующей диаграммой:

Матрица Вида

Давайте еще раз прочитаем цитату из футурамы:

«Двигатель не двигает корабль. Корабль остается на месте, а двигатели двигают вселенную вокруг него.»

То же самое можно применить и к фотоаппарату. Если вы хотите сфотографировать гору под каким-нибудь углом, то можно передвинуть фотокамеру…или гору. В реальной жизни это невозможно, но очень легко и удобно в компьютерной графике.

По умолчанию наша камера находится в центре Мировых Координат. Чтобы двигать наш мир нужно создать новую матрицу. К примеру нам нужно переместить нашу камеру на 3 единицы вправо(+Х). Это то же самое, что переместить весь мир на 3 единицы влево(-Х). И пока ваши мозги плавятся, давайте попробуем:

// Используйте #include и #include

glm::mat4 ViewMatrix = glm::translate(-3.0f, 0.0f ,0.0f);

Картинка ниже демонстрирует это: мы переходим от Мирового пространства(все вершины заданы относительно центра мира как мы это делали в предыдущей секции) к пространству камеры(все вершины заданы относительно камеры).

И прежде чем ваша голова совсем взорвется, посмотрите на прекрасную функцию из нашей старой доброй GLM:

glm::mat4 CameraMatrix = glm::LookAt(

cameraPosition , // Позиция камеры в мировых координатах

cameraTarget , // точка на которую мы хотим посмотреть в мировых координатах

upVector // скорее всего glm :: vec 3(0,1,0), а (0,-1,0) будет все показывать вверх ногами, что иногда тоже прикольно.

Вот иллюстрация к вышесказанному:

Но к нашей радости, это еще не все.

Матрица Проекции

Сейчас мы имеем координаты в пространстве камеры. Это значит, что после всех этих трансформаций, вершина которой посчастливилось оказаться в x==0 и y==0 будет отрендерена в центре экрана. Но мы же не можем пользоваться лишь координатами X,Y, чтобы понять куда рисовать вершину: дистанция к камере(Z) должна тоже учитываться! Если у нас есть две вершины, то одна из них будет более ближе к центру экрана чем другая, так как у неё больше координата Z.

Это называется перспективная проекция:

И к большому счастью для нас, матрица 4х4 может представлять собой и перспективные трансформации:

glm::mat4 projectionMatrix = glm::perspective(

FoV , // Горизонтальное Поле Вида в градусах. Или величина приближения . Как будто « линза » на камере . Обычно между 90(суперширокий, как рыбий глаз) и 30(как небольшая подзорная труба)

4.0 f / 3.0 f , // Соотношение сторон. Зависит от размера вашего окна. Например, 4/3 == 800/600 == 1280/960, знакомо, не правда ли?

0.1 f , // Ближнее поле отсечения. Его нужно задавать как можно большим, иначе будут проблемы с точностью.

100.0 f // Дальнее поле отсечения. Нужно держать как можно меньшим.

);

Повторим то что мы сейчас сделали:

Мы ушли от пространства камеры(все вершины заданы в координатах относительно камеры) в гомогенное пространство(все вершины в координатах маленького куба(-1,1). Все что находится в кубе – находится на экране.)

И финальная диаграмма:

Вот еще одна картинка чтобы стало яснее, что же происходит, когда мы умножаем всю эту проекционную матричную ерунду. Перед умножением на проекционную матрицу у нас есть голубые объекты заданные в пространстве камеры и красный объект, который представляет собой поле вида камеры: пространство которое попадает в объектив камеры:

После умножения на проекционную матрицу у нас выходит следующее:

На предыдущей картинке поле вида превратилось в идеальный куб(с координатами вершин от -1 до 1 по всем осям.), а все объекты деформированы в перспективе. Все голубые объекты которые близко к камере – стали большими, а которые дальше – маленькими. Так же как и в жизни!

Вот какой вид у нас открывается из «объектива»:

Однако оно квадратное, и нужно применить еще одно математическое преобразование, чтобы подогнать картинку под размеры окна.