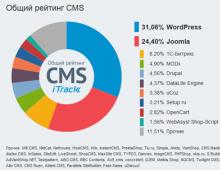
Construiți suprafețe la nivel de funcționalitate. Derivată a unei funcții specificată implicit
Definiție. Să fie n variabile și fiecare set de valori ale acestora (x X , X 2 ,..., X P ) dintr-un setXcorespunde unei valori bine definite a unei variabilez. Apoi spunem că este dată o funcție a mai multor variabilez= f(X X , X 2 ,..., X P ) .
Variabile X X , X 2 ,..., X P sunt numite variabile independente sau argumente,z - variabilă dependentă, un simbol f mijloace legea corespondenței. O multime de X numit domeniul de definire a funcției. Evident, acesta este un subset al spațiului n-dimensional.
Se notează o funcție a două variabile z=f(x, y). Atunci domeniul său de definiție X este o submulțime a planului de coordonate Ohoo.
Vecinătatea unui punct 
se numeste un cerc care contine un punct
(vezi Fig. 1).
Evident, un cerc pe un plan este un analog bidimensional al unui interval pe o linie dreaptă.
La studierea funcţiilor mai multor variabile se foloseşte aparatul matematic: orice funcţie z=
f(X, y) se poate asocia o pereche de functii ale unei variabile: cu o valoare fixa x=x 0
funcţie z=
și pentru o valoare fixă y=y 0
funcţie z=
f(X, y 0
).
Graficul unei funcții a două variabile
z=
numită mulţimea punctelor din spaţiul tridimensional (x, y, z), aplicate z care este asociat cu abscisa X si ordonata la relație funcțională z=
.
Pentru a reprezenta grafic o funcție z=f(x, y) este util să luăm în considerare funcțiile unei variabile z=
f(X, y 0
) Și z=
, reprezentând secțiuni Arte grafice z=
f(X, y) plane paralele cu planurile de coordonate OxzȘi Oyz, adică avioane y=la 0
Și x=x 0
.
Exemplul 1. Reprezentați grafic o funcție 
.
Soluţie. Secțiuni de suprafață 
=
plane paralele cu planurile de coordonate OyzȘi Oxz, reprezintă parabole (de exemplu, la x = 0
, cu y = 1 
etc.). Într-o secțiune a unei suprafețe după un plan de coordonate Ohoo, adică avion z=0, rezultatul este un cerc 
Graficul funcției reprezintă o suprafață numită paraboloid (vezi Fig. 2)
Definiție. Linie de nivel funcţiile a două variabile z=f(x, y) este mulțimea de puncte de pe plan astfel încât în toate aceste puncte valoarea funcției să fie aceeași și egală cu C. Numărul C în acest caz se numește nivel.
Figura 3 prezintă liniile de nivel corespunzătoare valorilor C=1 și C=2. După cum puteți vedea, linia de nivel 
constă din două curbe disjunse. Linia 
– curbă de auto-intersectare.
Multe exemple de linii de nivel sunt bine cunoscute și familiare. De exemplu, paralelele și meridianele de pe un glob sunt linii la nivelul funcțiilor de latitudine și longitudine. Meteorologii publică hărți care arată izoterme - linii de temperatură.
Exemplul 2. Construiți linii de nivel de funcție 
.
Soluţie. Linie de nivel z=
C
aceasta este o curbă pe un plan Ooh, dat de ecuaţie X 2
+ la 2
- 2y = C sau X 2
+ (y - I) 2 = C+1. Aceasta este ecuația unui cerc cu centrul în punctul (0; 1) și raza 
(Fig. 4).
Punctul (0; 1) este o linie de nivel degenerată corespunzătoare valorii minime a funcției z=-1 și atins în punctul (0; 1). Liniile de nivel sunt cercuri concentrice, a căror rază crește odată cu creșterea z= C, Mai mult, distanțele dintre liniile cu același pas de nivel scad odată cu distanța față de centru. Liniile de nivel vă permit să vizualizați graficul acestei funcții, care a fost reprezentat anterior în Fig. 2.
Derivate parțiale
Să dăm argumentul X creştere ∆х, argument y - creştere ∆у. Apoi funcția z va primi valoarea incrementată f (x+∆x, y+∆y). Magnitudinea ∆ z= f(X+∆ X, y+∆ y)- f{ X, y) numit increment complet al funcției la punct (X y). Dacă specificați doar incrementul argumentului X sau doar increment de argument y, apoi incrementele rezultate ale funcției sunt numite corespunzător privat.
Incrementul total al unei funcții, în general, nu este egal cu suma câterilor, adică. 
Exemplul 15.6. Găsiți incrementele parțiale și totale ale unei funcții z= X y.
Soluţie. ;;.
Am inteles 
Definiție.Derivată parțială a unei funcții a mai multor variabile conform uneia dintre aceste variabile, limita raportului dintre incrementul parțial corespunzător al unei funcții și incrementul variabilei independente luate în considerare se numește deoarece aceasta din urmă tinde spre zero (dacă există această limită).
Derivata parțială se notează după cum urmează: 
sau 
, sau 
.
Pentru a găsi derivata
trebuie să considerăm constanta variabilă y și să găsim
-variabila x.În acest caz, se păstrează regulile cunoscute de diferențiere.
Exemplu. Găsiți derivate parțiale ale unei funcții:
A) z=
X
ln y+
.
Rezolvare: Pentru a găsi derivata parțială în raport cu X, noi gândim la valoare constantă. Prin urmare, 
.
În mod similar, diferențierea cu privire la y, noi gândim X o valoare constantă, adică 
.
Diferenţial de funcţie
Definiție.Diferenţial de funcţie este suma produselor derivatelor parțiale ale acestei funcții cu incrementele variabilelor independente corespunzătoare, acestea.
dz=
.
(1)
Considerând că pentru funcțiile f(x, y)=x,g(X, y)=y conform (1) df=
dx=∆
X;
dg=
dy=∆
y
formula diferenţială (1) poate fi scrisă ca dz=
z"
X
dx+
z"
y
dy
(2)
sau 
Definiție.Funcţiez=
f(X, y) se numeștediferentiabil
în punctul (x, y), dacă incrementul său total poate fi reprezentat ca(3),
Undedz
- functie diferentiala, – ,infinitesimala la 
.
Suficient condiția de diferențiabilitate a unei funcții a două variabile.
Teorema.Dacă derivatele parțiale ale funcțieiz" v (X, y) există în vecinătatea punctului (x, y) și sunt continue în punctul (x, y), atunci funcțiaz= f{ X, y) este diferențiabilă în acest punct.
La prelucrarea datelor în domeniile subiectuluiîn legătură cu activitate științifică, este adesea nevoie de a construi și de a vizualiza o funcție a două variabile independente. Un exemplu tipic este nevoia reprezentare vizuala rezultate ale rezolvării bidimensionale ecuatii diferentialeîn derivate parțiale, obținute sub formă de așa-numite funcții grid.
Se propune o clasă simplă pentru construirea liniilor de nivel (izoline) ale funcției: Z=F(X,Y) sub formă de linii pe avion X-Y, satisfacând ecuațiile Z=const (unde const este o mulțime de valori date).
Se presupune că funcția Z este specificată ca o matrice z pe o grilă arbitrară cu celule patruunghiulare. Grila este specificată de două tablouri x, y, unde J și K sunt dimensiunile grilei.
Valorile funcției sunt definite în colțurile celulei patrulatere. În fiecare celulă se verifică trecerea liniei de nivel calculate prin fețele sale și, cu condiția ca linia să treacă prin celulă, se calculează coordonatele intersecției liniei de nivel cu fețele. În interiorul celulei, linia este trasată ca un segment drept.
Textul sursă este prevăzut cu comentarii detaliate.
Fișier LinesLevels.cs:
Utilizarea System.Collections.Generic; folosind System.Linq; folosind System.Windows; namespace WpfLinesLevels ( clasă publică LinesOfLevels ( private int J, K; private double[,] X; private double[,] Y; private double[,] Z; // Lista izoliniilor Public List
Pentru a demonstra cum funcționează clasa, este oferită o mică aplicație de testare WPF care construiește linii de nivel pentru o funcție de forma: z = x^2 + y^2 pe o grilă de 10 pe 10.
Fișierul MainWindow.xaml:
Și fișierul de cod MainWindow.xaml.cs:
Folosind System.Linq; folosind System.Windows; folosind System.Windows.Controls; folosind System.Windows.Media; folosind System.Windows.Shapes; spațiu de nume WpfLinesLevels ( ///
Rezultatul exemplului de testare este prezentat în figură.
Dacă fiecare punct X = (x 1, x 2, ... x n) din mulțimea (X) de puncte ale spațiului n-dimensional este asociat cu o valoare bine definită a variabilei z, atunci ei spun că dat funcţie a n variabile z = f(x 1, x 2, ...x n) = f (X).
În acest caz, se numesc variabilele x 1, x 2, ... x n variabile independente sau argumente funcții, z - variabilă dependentă, iar simbolul f denotă legea corespondenței. Mulțimea (X) este numită domeniul definirii funcții (aceasta este un anumit subset al spațiului n-dimensional).
De exemplu, funcția z = 1/(x 1 x 2) este o funcție a două variabile. Argumentele sale sunt variabilele x 1 și x 2, iar z este variabila dependentă. Domeniul de definiție este întregul plan de coordonate, cu excepția dreptelor x 1 = 0 și x 2 = 0, adică. fără axele x și ordonate. Substituind orice punct din domeniul definiției în funcție, conform legii corespondenței pe care o obținem un anumit număr. De exemplu, luând punctul (2; 5), i.e. x 1 = 2, x 2 = 5, obținem
z = 1/(2*5) = 0,1 (adică z(2; 5) = 0,1).
O funcție de forma z = a 1 x 1 + a 2 x 2 + ... + a n x n + b, unde a 1, a 2,... și n, b sunt numere constante, se numește liniar. Poate fi considerată ca suma a n funcții liniare ale variabilelor x 1, x 2, ... x n. Toate celelalte funcții sunt numite neliniară.
De exemplu, funcția z = 1/(x 1 x 2) este neliniară, iar funcția z =
= x 1 + 7x 2 - 5 – liniar.
Orice funcție z = f (X) = f(x 1, x 2, ... x n) poate fi asociată cu n funcții ale unei variabile dacă fixăm valorile tuturor variabilelor, cu excepția uneia.
De exemplu, funcțiile a trei variabile z = 1/(x 1 x 2 x 3) pot fi asociate cu trei funcții ale unei variabile. Dacă fixăm x 2 = a și x 3 = b, atunci funcția va lua forma z = 1/(abx 1); dacă fixăm x 1 = a și x 3 = b, atunci va lua forma z = 1/(abx 2); dacă fixăm x 1 = a și x 2 = b, atunci va lua forma z = 1/(abx 3). În acest caz, toate cele trei funcții au aceeași formă. Nu este întotdeauna așa. De exemplu, dacă pentru o funcție a două variabile fixăm x 2 = a, atunci va lua forma z = 5x 1 a, adică. functie de putere, iar dacă fixăm x 1 = a, atunci va lua forma, i.e. functie exponentiala.
Programa funcția a două variabile z = f(x, y) este mulțimea de puncte din spațiul tridimensional (x, y, z), a căror aplicație z este legată de abscisa x și ordonată y printr-o relație funcțională
z = f (x, y). Acest grafic reprezintă o suprafață din spațiul tridimensional (de exemplu, ca în Figura 5.3).
Se poate dovedi că dacă o funcție este liniară (adică z = ax + by + c), atunci graficul ei este un plan în spațiul tridimensional. Alte exemple Grafice 3D Se recomandă studiul independent folosind manualul lui Kremer (pp. 405-406).
Dacă există mai mult de două variabile (n variabile), atunci programa funcția este o mulțime de puncte din spațiul (n+1)-dimensional pentru care coordonata x n+1 este calculată în conformitate cu o lege funcțională dată. Un astfel de grafic se numește hipersuprafață(Pentru funcție liniară – hiperplan), și reprezintă, de asemenea, o abstractizare științifică (este imposibil să o înfățișăm).
Figura 5.3 – Graficul unei funcții a două variabile în spațiul tridimensional
Suprafață plană o funcție de n variabile este o mulțime de puncte din spațiul n-dimensional astfel încât în toate aceste puncte valoarea funcției este aceeași și egală cu C. Numărul C însuși în acest caz se numește nivel.
De obicei, pentru aceeași funcție, este posibil să se construiască un număr infinit de suprafețe de nivel (corespunzător unor niveluri diferite).
Pentru o funcție de doi suprafata variabila nivelul ia forma linii de nivel.
De exemplu, să considerăm z = 1/(x 1 x 2). Să luăm C = 10, adică. 1/(x 1 x 2) = 10. Atunci x 2 = 1/(10x 1), adică. pe plan linia de nivel va lua forma prezentată în Figura 5.4 ca o linie continuă. Luând un alt nivel, de exemplu, C = 5, obținem linia nivelului sub forma unui grafic al funcției x 2 = 1/(5x 1) (prezentată cu o linie punctată în Figura 5.4).
Figura 5.4 - Linii de nivel de funcție z = 1/(x 1 x 2)
Să ne uităm la un alt exemplu. Fie z = 2x 1 + x 2. Să luăm C = 2, adică 2x 1 + x 2 = 2. Atunci x 2 = 2 - 2x 1, adică. pe plan linia de nivel va lua forma unei drepte, reprezentată în figura 5.5 printr-o linie continuă. Luând un alt nivel, de exemplu, C = 4, obținem o linie de nivel sub forma unei linii drepte x 2 = 4 - 2x 1 (prezentată cu o linie punctată în Figura 5.5). Linia de nivel pentru 2x 1 + x 2 = 3 este prezentată în Figura 5.5 sub formă de linie punctată.
Este ușor de verificat că pentru o funcție liniară a două variabile, orice linie de nivel va fi o linie dreaptă pe plan și toate liniile de nivel vor fi paralele între ele.
Figura 5.5 - Linii de nivel de funcție z = 2x 1 + x 2
Definirea unei funcții a mai multor variabile
Când luăm în considerare funcțiile unei variabile, am subliniat că atunci când studiem mai multe fenomene trebuie să întâlnim funcții a două sau mai multe variabile independente. Să dăm câteva exemple.
Exemplul 1. Pătrat S dreptunghi cu laturile ale căror lungimi sunt egale XȘi la, se exprimă prin formula S = X y. Fiecare pereche de valori XȘi la corespunde unei anumite valori de suprafață S; S este o funcție a două variabile.
Exemplul 2. Volum V paralelipiped dreptunghiular cu muchii ale căror lungimi sunt egale X, la, z, se exprimă prin formula V= xyz. Aici V există o funcție a trei variabile X, la, z.
Exemplul 3.
Gamă R zborul de proiectile trase cu viteza inițială v 0 de la un pistol a cărui țeavă este înclinată pe orizontală la un unghi se exprimă prin formula 
(dacă neglijăm rezistența aerului). Aici g– accelerarea gravitației. Pentru fiecare pereche de valori v 0 și această formulă dă o anumită valoare R, adică R este o funcție a două variabile v 0 și .
Exemplul 4.
. Aici Și există o funcție a patru variabile X, la, z, t.
Definiția 1. Dacă fiecare pereche ( X, la) valorile a două variabile independente una de cealaltă XȘi la dintr-un anumit domeniu al schimbării lor D, corespunde unei anumite valori a cantității z, atunci spunem asta z exista o functie două variabile independente xȘi la, definită în zonă D.
Simbolic, o funcție a două variabile se notează după cum urmează:
z= f(X, y), z = F(X, y) etc.
O funcție a două variabile poate fi specificată, de exemplu, folosind un tabel sau analitic - folosind o formulă, așa cum sa făcut în exemplele discutate mai sus. Pe baza formulei, puteți crea un tabel de valori ale funcției pentru unele perechi de valori ale variabilelor independente. Deci, pentru primul exemplu, puteți crea următorul tabel:
S = X y
În acest tabel, la intersecția unui rând și a unei coloane corespunzătoare anumitor valori XȘi la, este introdusă valoarea funcției corespunzătoare S. Dacă dependenta functionala z= f(X, y) se obţine în urma măsurătorilor mărimii z La studierea experimentală a oricărui fenomen, se obține imediat un tabel care determină zîn funcţie de două variabile. În acest caz, funcția este specificată numai de tabel.
Ca și în cazul unei variabile independente, o funcție a două variabile nu există, în general, pentru nicio valoare. XȘi la.
Definiția 2. Un set de perechi ( X, la) valori XȘi la, la care se determină funcția z= f(X, y), numit domeniul definirii sau zona de existenta această funcție.
Domeniul de definire al unei funcții este clar ilustrat geometric. Dacă fiecare pereche de valori XȘi la o vom reprezenta cu un punct M(X, la) in avion Ohoo, atunci domeniul de definire al funcției va fi reprezentat ca o anumită colecție de puncte din plan. Vom numi și această colecție de puncte domeniul de definire a funcției. În special, domeniul definiției poate fi întregul plan. În cele ce urmează ne vom ocupa în principal de domenii care reprezintă părți ale avionului, delimitate de linii. Linia de limitare aceasta zona, vom suna frontieră zone. Vor fi numite puncte ale regiunii care nu se află la graniță intern puncte ale zonei. Se numește o zonă constând doar din puncte interioare deschis sau deschis. Dacă și punctele de limită aparțin regiunii, atunci regiunea este numită închis. O zonă se numește mărginită dacă există o astfel de constantă CU, că distanța oricărui punct M zona de la origine DESPRE Mai puțin CU, adică | OM| < CU.
Exemplul 5. Determinați domeniul natural al unei funcții
z = 2X – la.
Expresia analitică 2 X – la are sens pentru orice valoare XȘi la. În consecință, domeniul natural de definire al funcției este întregul plan Ohoo.
Exemplul 6.
.
Pentru a z a avut valoare reala, este necesar ca rădăcina să aibă un număr nenegativ, adică. XȘi la trebuie să satisfacă inegalitatea 1 – X 2 – la 2 0 sau X 2 + la 2 1.
Toate punctele M(X, la), ale căror coordonate satisfac inegalitatea indicată, se află într-un cerc de rază 1 cu un centru la origine și la limita acestui cerc.
Exemplul 7.
.
Deoarece logaritmii sunt definiți numai pentru numere pozitive, inegalitatea trebuie satisfăcută X + la> 0 sau la > X.
Aceasta înseamnă că domeniul de definire al funcției z este jumătatea planului situată deasupra liniei la = X, fără a include linia dreaptă în sine.
Exemplul 8. Aria unui triunghi S reprezintă funcția de bază Xși înălțimi la: S= X y/2.
Domeniul de definire al acestei funcții este domeniul X 0, la 0 (deoarece baza unui triunghi și înălțimea lui nu pot fi nici negative, nici zero). Rețineți că domeniul de definire al funcției luate în considerare nu coincide cu domeniul natural de definire al expresiei analitice cu care este specificată funcția, deoarece domeniul natural de definire al expresiei X y/ 2 este, evident, întregul avion Ohoo.
Definiția unei funcții a două variabile poate fi generalizată cu ușurință în cazul a trei sau mai multe variabile.
Definiția 3. Dacă fiecare considerat set de valori variabile X, la, z, …, u, t corespunde unei anumite valori variabile w, atunci vom suna w funcţia variabilelor independente X, la, z, …, u, t si scrie w= F(X, la, z, …, u, t) sau w= f(X, la, z, …, u, t) și așa mai departe.
La fel ca și pentru o funcție de două variabile, putem vorbi despre domeniul de definire al unei funcții de trei, patru sau mai multe variabile.
Deci, de exemplu, pentru funcția de trei zonă variabilă Definiția este o anumită colecție de triple de numere ( X, la, z). Să observăm imediat că fiecare triplu de numere definește un anumit punct M(X, la, z) in spatiu Ohooz. În consecință, domeniul de definire a unei funcții de trei variabile este un anumit set de puncte din spațiu.
În mod similar, putem vorbi despre domeniul de definire al unei funcții de patru variabile u= f(X, y, z, t) ca despre o colecție de cvadruple de numere ( X, y, z, t). Cu toate acestea, domeniul de definire a unei funcții de patru sau Mai mult variabilele nu mai permit o interpretare geometrică simplă.
Exemplul 2 arată o funcție a trei variabile definite pentru toate valorile X, la, z.
Exemplul 4 arată o funcție a patru variabile.
Exemplul 9. .
Aici w– funcţia a patru variabile X, la, z, Și, definit cu valori ale variabilelor care satisfac relația:
Conceptul de funcție a mai multor variabile
Să introducem conceptul de funcție a mai multor variabile.
Definiția 1. Lasă fiecare punct M dintr-un set de puncte ( M) Spațiul euclidian Em conform unor legi, un anumit număr este pus în corespondență Și dintr-o mulţime numerică U. Apoi vom spune că pe platou ( M) este dată funcția și =f(M). Mai mult, seturile ( M) Și U se numesc, respectiv, domeniul definirii (atribuirii) si domeniul schimbarii functiei f(M).
După cum știți, o funcție a unei variabile la = f(X) este reprezentată în plan ca o linie. În cazul a două variabile, domeniul definiției ( M P) funcții z = f(x, y) reprezintă un set de puncte pe planul de coordonate Ohoo(Fig. 8.1). Coordona z numit aplica,și apoi funcția în sine este descrisă ca o suprafață în spațiu E3 . În mod similar, funcția de la T variabile
definit pe platou ( M) Spațiul euclidian Em, reprezintă o hipersuprafață în spațiul euclidian Em+1.
Unele tipuri de funcții ale mai multor variabile
Să ne uităm la exemple de funcții ale mai multor variabile și să găsim domeniile lor de definiție.
E3
.
Domeniul de definire al acestei funcții este întregul set de puncte al planului Ooh. Domeniul acestei funcții este intervalul )
