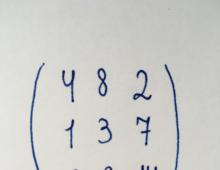Matrici. Tipuri de matrice. Conceptul de matrice În ce constă o matrice?

O matrice este un obiect special în matematică. Este reprezentat sub forma unui tabel dreptunghiular sau pătrat, compus dintr-un anumit număr de rânduri și coloane. În matematică există o mare varietate de tipuri de matrice, care variază ca mărime sau conținut. Numerele rândurilor și coloanelor sale se numesc ordine. Aceste obiecte sunt folosite în matematică pentru a organiza înregistrarea sistemelor de ecuații liniare și pentru a căuta în mod convenabil rezultatele acestora. Ecuațiile folosind o matrice sunt rezolvate folosind metoda lui Carl Gauss, Gabriel Cramer, adunări minore și algebrice, precum și multe alte metode. Abilitatea de bază atunci când lucrați cu matrici este reducerea la Cu toate acestea, mai întâi, să ne dăm seama ce tipuri de matrice se disting de matematicieni.

Tip nul

Toate componentele acestui tip de matrice sunt zerouri. Între timp, numărul rândurilor și coloanelor sale este complet diferit.

Tip pătrat

Numărul de coloane și rânduri ale acestui tip de matrice este același. Cu alte cuvinte, este o masă în formă de „pătrat”. Numărul coloanelor (sau rândurilor) sale se numește ordine. Cazurile speciale sunt considerate a fi existența unei matrice de ordinul doi (matrice 2x2), de ordinul al patrulea (4x4), de ordinul al zecelea (10x10), de ordinul al șaptesprezecelea (17x17) și așa mai departe.

Vector coloană

Acesta este unul dintre cele mai simple tipuri de matrice, care conține o singură coloană, care include trei valori numerice. Reprezintă un număr de termeni liberi (numere independente de variabile) în sisteme de ecuații liniare.

Vedere similară cu cea anterioară. Constă din trei elemente numerice, la rândul lor organizate într-o singură linie.

Tip diagonal

Valorile numerice în forma diagonală a matricei iau numai componentele diagonalei principale (evidențiate cu verde). Diagonala principală începe cu elementul situat în colțul din stânga sus și se termină cu elementul din dreapta jos, respectiv. Componentele rămase sunt egale cu zero. Tipul diagonal este doar o matrice pătrată de un anumit ordin. Dintre matricele diagonale se poate distinge pe cea scalară. Toate componentele sale iau aceleași valori.

Un subtip de matrice diagonală. Toate valorile sale numerice sunt unități. Folosind un singur tip de tabel matrice, se efectuează transformările sale de bază sau se găsește o matrice inversă celei originale.

Tip canonic

Forma canonică a matricei este considerată una dintre cele principale; Reducerea la acesta este adesea necesară pentru muncă. Numărul de rânduri și coloane dintr-o matrice canonică variază și nu aparține neapărat tipului pătrat. Este oarecum similar cu matricea de identitate, dar în cazul ei nu toate componentele diagonalei principale iau o valoare egală cu unu. Pot exista două sau patru unități diagonale principale (totul depinde de lungimea și lățimea matricei). Sau este posibil să nu existe deloc unități (atunci este considerat zero). Componentele rămase de tip canonic, precum și elementele diagonale și unitare, sunt egale cu zero.

Tip triunghiular

Unul dintre cele mai importante tipuri de matrice, folosit la căutarea determinantului său și la efectuarea unor operații simple. Tipul triunghiular provine din tipul diagonal, deci matricea este și pătrată. Tipul triunghiular de matrice este împărțit în triunghiular superior și triunghiular inferior.

Într-o matrice triunghiulară superioară (Fig. 1), numai elementele care se află deasupra diagonalei principale iau o valoare egală cu zero. Componentele diagonalei în sine și partea matricei situată sub ea conțin valori numerice.

În matricea triunghiulară inferioară (Fig. 2), dimpotrivă, elementele situate în partea inferioară a matricei sunt egale cu zero.

Tipul este necesar pentru a găsi rangul unei matrice, precum și pentru operații elementare asupra acestora (împreună cu tipul triunghiular). Matricea pașilor este numită așa deoarece conține „pași” caracteristici de zerouri (așa cum se arată în figură). În tipul de pas, se formează o diagonală de zerouri (nu neapărat cea principală), iar toate elementele de sub această diagonală au, de asemenea, valori egale cu zero. O condiție prealabilă este următoarea: dacă există un rând zero în matricea pașilor, atunci rândurile rămase de sub acesta nu conțin nici valori numerice.

Astfel, am examinat cele mai importante tipuri de matrice necesare pentru a lucra cu acestea. Acum să ne uităm la problema conversiei matricei în forma necesară.

Reducerea la forma triunghiulara

Cum se aduce o matrice într-o formă triunghiulară? Cel mai adesea în sarcini trebuie să transformați o matrice într-o formă triunghiulară pentru a-i găsi determinantul, altfel numit determinant. Atunci când se efectuează această procedură, este extrem de important să se „pastreze” diagonala principală a matricei, deoarece determinantul unei matrice triunghiulare este egal cu produsul componentelor diagonalei sale principale. Permiteți-mi să reamintesc și metode alternative de găsire a determinantului. Determinantul tipului pătrat se găsește folosind formule speciale. De exemplu, puteți folosi metoda triunghiului. Pentru alte matrici se folosește metoda de descompunere pe rând, coloană sau elementele acestora. De asemenea, puteți utiliza metoda minorilor și adăugărilor de matrice algebrică.

Să analizăm în detaliu procesul de reducere a unei matrice la o formă triunghiulară folosind exemple ale unor sarcini.

Exercitiul 1

Este necesar să se găsească determinantul matricei prezentate folosind metoda reducerii acesteia la formă triunghiulară.

Matricea dată nouă este o matrice pătrată de ordinul trei. Prin urmare, pentru a o transforma într-o formă triunghiulară, va trebui să scoatem la zero două componente ale primei coloane și o componentă a celei de-a doua.

Pentru a-l aduce la formă triunghiulară, începem transformarea din colțul din stânga jos al matricei - de la numărul 6. Pentru a o transforma la zero, înmulțiți primul rând cu trei și scădeți-l din ultimul rând.

Important! Rândul de sus nu se modifică, dar rămâne același ca în matricea originală. Nu este nevoie să scrieți un șir de patru ori mai mare decât cel original. Dar valorile șirurilor ale căror componente trebuie setate la zero se schimbă constant.

Rămâne doar ultima valoare - elementul celui de-al treilea rând al celei de-a doua coloane. Acesta este numărul (-1). Pentru a-l transforma la zero, scade pe al doilea din prima linie.

Sa verificam:

detA = 2 x (-1) x 11 = -22.

Aceasta înseamnă că răspunsul la sarcină este -22.

Sarcina 2

Este necesar să se găsească determinantul matricei reducându-l la formă triunghiulară.

Matricea prezentată aparține tipului pătrat și este o matrice de ordinul al patrulea. Aceasta înseamnă că este necesar să transformați trei componente ale primei coloane, două componente ale celei de-a doua coloane și o componentă a celei de-a treia la zero.

Să începem să o reducem cu elementul situat în colțul din stânga jos - cu numărul 4. Trebuie să transformăm acest număr la zero. Cel mai simplu mod de a face acest lucru este să înmulțiți linia de sus cu patru și apoi să o scădeți din a patra. Să notăm rezultatul primei etape de transformare.

Deci, componenta al patrulea rând este setată la zero. Să trecem la primul element al celei de-a treia rânduri, la numărul 3. Efectuăm o operație similară. Înmulțim prima linie cu trei, o scădem din a treia linie și notăm rezultatul.

Am reușit să întoarcem la zero toate componentele primei coloane a acestei matrice pătrate, cu excepția numărului 1 - un element al diagonalei principale care nu necesită transformare. Acum este important să păstrăm zerourile rezultate, așa că vom efectua transformările cu rânduri, nu cu coloane. Să trecem la a doua coloană a matricei prezentate.

Să începem din nou din partea de jos - cu elementul coloanei a doua a ultimului rând. Acest număr este (-7). Cu toate acestea, în acest caz, este mai convenabil să începeți cu numărul (-1) - elementul coloanei a doua a celui de-al treilea rând. Pentru a-l transforma la zero, scădeți al doilea din a treia linie. Apoi înmulțim a doua linie cu șapte și o scadem din a patra. Am primit zero în loc de elementul situat în al patrulea rând al celei de-a doua coloane. Acum să trecem la a treia coloană.

În această coloană, trebuie să transformăm doar un număr la zero - 4. Acest lucru nu este dificil de făcut: pur și simplu adăugăm o treime la ultima linie și vedem zeroul de care avem nevoie.

După toate transformările făcute, am adus matricea propusă într-o formă triunghiulară. Acum, pentru a-i găsi determinantul, trebuie doar să înmulți elementele rezultate ale diagonalei principale. Primim: detA = 1 x (-1) x (-4) x 40 = 160. Prin urmare, soluția este 160.

Deci, acum problema reducerii matricei la formă triunghiulară nu vă va deranja.

Reducerea la o formă în trepte

Pentru operațiile elementare pe matrice, forma în trepte este mai puțin „la cerere” decât cea triunghiulară. Cel mai adesea este folosit pentru a găsi rangul unei matrice (adică numărul rândurilor sale diferite de zero) sau pentru a determina rânduri dependente și independente liniar. Cu toate acestea, tipul de matrice în trepte este mai universal, deoarece este potrivit nu numai pentru tipul pătrat, ci și pentru toate celelalte.

Pentru a reduce o matrice la forma treptat, mai întâi trebuie să găsiți determinantul acesteia. Metodele de mai sus sunt potrivite pentru aceasta. Scopul găsirii determinantului este de a afla dacă acesta poate fi convertit într-o matrice de etape. Dacă determinantul este mai mare sau mai mic decât zero, atunci puteți trece în siguranță la sarcină. Dacă este egal cu zero, nu va fi posibilă reducerea matricei la o formă în trepte. În acest caz, trebuie să verificați dacă există erori în înregistrare sau în transformările matricei. Dacă nu există astfel de inexactități, sarcina nu poate fi rezolvată.

Să ne uităm la cum să reduceți o matrice la o formă în pas folosind exemple de mai multe sarcini.

Exercitiul 1. Găsiți rangul tabelului matriceal dat.

În fața noastră este o matrice pătrată de ordinul trei (3x3). Știm că pentru a găsi rangul este necesar să-l reducem la o formă treptat. Prin urmare, mai întâi trebuie să găsim determinantul matricei. Să folosim metoda triunghiului: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1 x 1 x 4) - (2 x 3 x 0) - (6 x 5 x 2) = 12.

Determinant = 12. Este mai mare decât zero, ceea ce înseamnă că matricea poate fi redusă la o formă în trepte. Să începem să-l transformăm.

Să începem cu elementul coloanei din stânga a celei de-a treia linii - numărul 2. Înmulțiți linia de sus cu două și scădeți-o din a treia. Datorită acestei operații, atât elementul de care avem nevoie, cât și numărul 4 - elementul coloanei a doua a celui de-al treilea rând - s-au transformat la zero.

Vedem că în urma reducerii s-a format o matrice triunghiulară. În cazul nostru, nu putem continua transformarea, deoarece componentele rămase nu pot fi reduse la zero.

Aceasta înseamnă că concluzionăm că numărul de rânduri care conțin valori numerice în această matrice (sau rangul acesteia) este 3. Răspunsul la sarcină: 3.

Sarcina 2. Determinați numărul de rânduri liniar independente ale acestei matrice.

Trebuie să găsim șiruri care nu pot fi convertite la zero prin nicio transformare. De fapt, trebuie să găsim numărul de rânduri diferite de zero sau rangul matricei prezentate. Pentru a face acest lucru, să simplificăm.

Vedem o matrice care nu aparține tipului pătrat. Măsoară 3x4. Să începem și reducerea cu elementul din colțul din stânga jos - numărul (-1).

Transformările sale ulterioare sunt imposibile. Aceasta înseamnă că concluzionăm că numărul de linii liniar independente din el și răspunsul la sarcină este 3.

Acum, reducerea matricei la o formă în trepte nu este o sarcină imposibilă pentru tine.

Folosind exemple ale acestor sarcini, am examinat reducerea unei matrice la o formă triunghiulară și o formă în trepte. Pentru a transforma valorile dorite ale tabelelor matrice la zero, în unele cazuri trebuie să vă folosiți imaginația și să convertiți corect coloanele sau rândurile acestora. Mult succes la matematică și la lucrul cu matrice!

Acest subiect va acoperi operațiuni precum adunarea și scăderea matricelor, înmulțirea unei matrice cu un număr, înmulțirea unei matrice cu o matrice și transpunerea unei matrice. Toate simbolurile folosite pe această pagină sunt preluate din subiectul anterior.

Adunarea și scăderea matricelor.

Suma $A+B$ a matricelor $A_(m\times n)=(a_(ij))$ și $B_(m\times n)=(b_(ij))$ se numește matrice $C_(m \times n) =(c_(ij))$, unde $c_(ij)=a_(ij)+b_(ij)$ pentru toate $i=\overline(1,m)$ și $j=\overline( 1,n) $.

O definiție similară este introdusă pentru diferența de matrice:

Diferența dintre matricele $A-B$ $A_(m\times n)=(a_(ij))$ și $B_(m\times n)=(b_(ij))$ este matricea $C_(m\times n)=( c_(ij))$, unde $c_(ij)=a_(ij)-b_(ij)$ pentru toți $i=\overline(1,m)$ și $j=\overline(1, n)$.

Explicație pentru intrarea $i=\overline(1,m)$: show\hide

Notația „$i=\overline(1,m)$” înseamnă că parametrul $i$ variază de la 1 la m. De exemplu, notația $i=\overline(1,5)$ indică faptul că parametrul $i$ ia valorile 1, 2, 3, 4, 5.

Este de remarcat faptul că operațiile de adunare și scădere sunt definite numai pentru matrice de aceeași dimensiune. În general, adunarea și scăderea matricelor sunt operații clare intuitiv, deoarece ele înseamnă în esență doar însumarea sau scăderea elementelor corespunzătoare.

Exemplul nr. 1

Sunt date trei matrice:

$$ A=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)\;\; B=\left(\begin(array) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right); \;\; F=\left(\begin(array) (cc) 1 & 0 \\ -5 & 4 \end(array) \right). $$

Este posibil să găsim matricea $A+F$? Găsiți matrice $C$ și $D$ dacă $C=A+B$ și $D=A-B$.

Matricea $A$ conține 2 rânduri și 3 coloane (cu alte cuvinte, dimensiunea matricei $A$ este $2\xtime 3$), iar matricea $F$ conține 2 rânduri și 2 coloane. Dimensiunile matricelor $A$ și $F$ nu se potrivesc, așa că nu le putem adăuga, adică. operația $A+F$ nu este definită pentru aceste matrici.

Dimensiunile matricelor $A$ și $B$ sunt aceleași, adică. Datele matricei conțin un număr egal de rânduri și coloane, astfel încât operația de adăugare este aplicabilă acestora.

$$ C=A+B=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)+ \left(\begin(array) ) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right)=\\= \left(\begin(array) (ccc) -1+10 & -2+( -25) & 1+98 \\ 5+3 & 9+0 & -8+(-14) \end(array) \right)= \left(\begin(array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \end(array) \right) $$

Să găsim matricea $D=A-B$:

$$ D=A-B=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)-\left(\begin(array) ( ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right)=\\= \left(\begin(array) (ccc) -1-10 & -2-(-25 ) & 1-98 \\ 5-3 & 9-0 & -8-(-14) \end(array) \right)= \left(\begin(array) (ccc) -11 & 23 & -97 \ \2 & 9 & 6 \end(array) \right) $$

Răspuns: $C=\left(\begin(array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \end(array) \right)$, $D=\left(\begin(array) (ccc) -11 & 23 & -97 \\ 2 & 9 & 6 \end(array) \right)$.

Înmulțirea unei matrice cu un număr.

Produsul matricei $A_(m\times n)=(a_(ij))$ cu numărul $\alpha$ este matricea $B_(m\times n)=(b_(ij))$, unde $ b_(ij)= \alpha\cdot a_(ij)$ pentru toți $i=\overline(1,m)$ și $j=\overline(1,n)$.

Mai simplu spus, înmulțirea unei matrice cu un anumit număr înseamnă înmulțirea fiecărui element dintr-o matrice dată cu acel număr.

Exemplul nr. 2

Matricea este dată: $ A=\left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right)$. Găsiți matrice $3\cdot A$, $-5\cdot A$ și $-A$.

$$ 3\cdot A=3\cdot \left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right) =\left(\begin( matrice) (ccc) 3\cdot(-1) și 3\cdot(-2) și 3\cdot 7 \\ 3\cdot 4 și 3\cdot 9 și 3\cdot 0 \end(array) \right)= \left(\begin(array) (ccc) -3 & -6 & 21 \\ 12& 27 & 0 \end(array) \right).\\ -5\cdot A=-5\cdot \left(\begin (matrice) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right) =\left(\begin(array) (ccc) -5\cdot(-1) & - 5\cdot(-2) & -5\cdot 7 \\ -5\cdot 4 & -5\cdot 9 & -5\cdot 0 \end(array) \right)= \left(\begin(array) ( ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \end(array) \right). $$

Notația $-A$ este o notație scurtă pentru $-1\cdot A$. Adică, pentru a găsi $-A$ trebuie să înmulțiți toate elementele matricei $A$ cu (-1). În esență, aceasta înseamnă că semnul tuturor elementelor matricei $A$ se va schimba în opus:

$$ -A=-1\cdot A=-1\cdot \left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right)= \ stânga(\begin(array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \end(array) \right) $$

Răspuns: $3\cdot A=\left(\begin(array) (ccc) -3 & -6 & 21 \\ 12& 27 & 0 \end(array) \right);\; -5\cdot A=\left(\begin(array) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \end(array) \right);\; -A=\left(\begin(array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \end(array) \right)$.

Produsul a două matrice.

Definiția acestei operațiuni este greoaie și, la prima vedere, neclară. Prin urmare, mai întâi voi indica o definiție generală, apoi vom analiza în detaliu ce înseamnă aceasta și cum să lucrăm cu ea.

Produsul matricei $A_(m\times n)=(a_(ij))$ de la matricea $B_(n\times k)=(b_(ij))$ este matricea $C_(m\times k )=(c_( ij))$, pentru care fiecare element $c_(ij)$ este egal cu suma produselor elementelor corespondente ale rândului i al matricei $A$ de elementele j -a coloană a matricei $B$: $$c_(ij)=\sum\limits_ (p=1)^(n)a_(ip)b_(pj), \;\; i=\overline(1,m), j=\overline(1,n).$$

Să ne uităm la înmulțirea matricei pas cu pas folosind un exemplu. Cu toate acestea, ar trebui să rețineți imediat că nu toate matricele pot fi multiplicate. Dacă dorim să înmulțim matricea $A$ cu matricea $B$, atunci trebuie mai întâi să ne asigurăm că numărul de coloane ale matricei $A$ este egal cu numărul de rânduri ale matricei $B$ (astfel de matrici sunt adesea numite ne-am înțeles asupra). De exemplu, matricea $A_(5\times 4)$ (matricea conține 5 rânduri și 4 coloane) nu poate fi înmulțită cu matricea $F_(9\times 8)$ (9 rânduri și 8 coloane), deoarece numărul de coloane ale matricei $A $ nu este egal cu numărul de rânduri ale matricei $F$, adică. $4\neq 9$. Dar puteți înmulți matricea $A_(5\times 4)$ cu matricea $B_(4\times 9)$, deoarece numărul de coloane ale matricei $A$ este egal cu numărul de rânduri ale matricei $ B$. În acest caz, rezultatul înmulțirii matricelor $A_(5\times 4)$ și $B_(4\times 9)$ va fi matricea $C_(5\times 9)$, care conține 5 rânduri și 9 coloane:

Exemplul nr. 3

Matrici date: $ A=\left(\begin(array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \end (matrice) \right)$ și $ B=\left(\begin(array) (cc) -9 și 3 \\ 6 și 20 \\ 7 și 0 \\ 12 și -4 \end (matrice) \right) $. Găsiți matricea $C=A\cdot B$.

Mai întâi, să determinăm imediat dimensiunea matricei $C$. Deoarece matricea $A$ are dimensiunea $3\x 4$, iar matricea $B$ are dimensiunea $4\x 2$, atunci dimensiunea matricei $C$ este: $3\x 2$:

Deci, ca rezultat al produsului matricelor $A$ și $B$, ar trebui să obținem o matrice $C$, formată din trei rânduri și două coloane: $ C=\left(\begin(array) (cc) c_ (11) și c_( 12) \\ c_(21) și c_(22) \\ c_(31) și c_(32) \end(array) \right)$. Dacă desemnarea elementelor ridică întrebări, atunci puteți privi subiectul anterior: „Matrice. Tipuri de matrice. Termeni de bază”, la începutul căruia este explicată desemnarea elementelor matriceale. Scopul nostru: să găsim valorile tuturor elementelor matricei $C$.

Să începem cu elementul $c_(11)$. Pentru a obține elementul $c_(11)$, trebuie să găsiți suma produselor elementelor din primul rând al matricei $A$ și prima coloană a matricei $B$:

Pentru a găsi elementul $c_(11)$ în sine, trebuie să înmulțiți elementele primului rând al matricei $A$ cu elementele corespunzătoare din prima coloană a matricei $B$, adică. primul element la primul, al doilea la al doilea, al treilea la al treilea, al patrulea la al patrulea. Rezumam rezultatele obtinute:

$$ c_(11)=-1\cdot (-9)+2\cdot 6+(-3)\cdot 7 + 0\cdot 12=0. $$

Să continuăm soluția și să găsim $c_(12)$. Pentru a face acest lucru, va trebui să înmulți elementele din primul rând al matricei $A$ și din a doua coloană a matricei $B$:

Similar cu precedentul, avem:

$$ c_(12)=-1\cdot 3+2\cdot 20+(-3)\cdot 0 + 0\cdot (-4)=37. $$

Toate elementele primului rând al matricei $C$ au fost găsite. Să trecem la a doua linie, care începe cu elementul $c_(21)$. Pentru a-l găsi, va trebui să înmulți elementele celui de-al doilea rând al matricei $A$ și prima coloană a matricei $B$:

$$ c_(21)=5\cdot (-9)+4\cdot 6+(-2)\cdot 7 + 1\cdot 12=-23. $$

Găsim următorul element $c_(22)$ înmulțind elementele celui de-al doilea rând al matricei $A$ cu elementele corespunzătoare din a doua coloană a matricei $B$:

$$ c_(22)=5\cdot 3+4\cdot 20+(-2)\cdot 0 + 1\cdot (-4)=91. $$

Pentru a găsi $c_(31)$, înmulțiți elementele celui de-al treilea rând al matricei $A$ cu elementele primei coloane a matricei $B$:

$$ c_(31)=-8\cdot (-9)+11\cdot 6+(-10)\cdot 7 + (-5)\cdot 12=8. $$

Și, în final, pentru a găsi elementul $c_(32)$, va trebui să înmulțiți elementele celui de-al treilea rând al matricei $A$ cu elementele corespunzătoare din a doua coloană a matricei $B$:

$$ c_(32)=-8\cdot 3+11\cdot 20+(-10)\cdot 0 + (-5)\cdot (-4)=216. $$

Toate elementele matricei $C$ au fost găsite, tot ce rămâne este să scrieți că $C=\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end( matrice) \right)$ . Sau, pentru a scrie integral:

$$ C=A\cdot B =\left(\begin(array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & - 5 \end(array) \right)\cdot \left(\begin(array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end(array) \right) =\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right). $$

Răspuns: $C=\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right)$.

Apropo, adesea nu există niciun motiv pentru a descrie în detaliu locația fiecărui element al matricei rezultate. Pentru matricele a căror dimensiune este mică, puteți face acest lucru:

$$ \left(\begin(array) (cc) 6 & 3 \\ -17 & -2 \end(array)\right)\cdot \left(\begin(array) (cc) 4 & 9 \\ - 6 și 90 \end(array) \right) =\left(\begin(array) (cc) 6\cdot(4)+3\cdot(-6) și 6\cdot(9)+3\cdot(90) ) \\ -17\cdot(4)+(-2)\cdot(-6) & -17\cdot(9)+(-2)\cdot(90) \end(array) \right) =\left (\begin(array) (cc) 6 și 324 \\ -56 și -333 \end(array) \right) $$

De asemenea, este de remarcat faptul că înmulțirea matricei este necomutativă. Aceasta înseamnă că în cazul general $A\cdot B\neq B\cdot A$. Numai pentru unele tipuri de matrice, care sunt numite permutabil(sau naveta), egalitatea $A\cdot B=B\cdot A$ este adevărată. Pe baza necomutativității înmulțirii trebuie să indicăm exact cum înmulțim expresia cu o anumită matrice: în dreapta sau în stânga. De exemplu, expresia „înmulțiți ambele părți ale egalității $3E-F=Y$ cu matricea $A$ din dreapta” înseamnă că doriți să obțineți următoarea egalitate: $(3E-F)\cdot A=Y\cdot A$.

Transpusă față de matricea $A_(m\times n)=(a_(ij))$ este matricea $A_(n\times m)^(T)=(a_(ij)^(T))$, pentru elementele care $a_(ij)^(T)=a_(ji)$.

Mai simplu spus, pentru a obține o matrice transpusă $A^T$, trebuie să înlocuiți coloanele din matricea originală $A$ cu rândurile corespunzătoare conform acestui principiu: a existat un prim rând - va fi o primă coloană ; a existat un al doilea rând - va fi o a doua coloană; a fost un al treilea rând - va fi o a treia coloană și așa mai departe. De exemplu, să găsim matricea transpusă în matricea $A_(3\times 5)$:

În consecință, dacă matricea originală a avut o dimensiune de $3\times 5$, atunci matricea transpusă are o dimensiune de $5\times 3$.

Unele proprietăți ale operațiilor pe matrice.

Aici se presupune că $\alpha$, $\beta$ sunt niște numere și $A$, $B$, $C$ sunt matrici. Pentru primele patru proprietăți am indicat nume; restul pot fi denumite prin analogie cu primele patru.

Definiția 1. Dimensiunea matricei Am n este un tabel dreptunghiular de m rânduri și n coloane, format din numere sau alte expresii matematice (numite elemente de matrice), i = 1,2,3,…,m, j = 1,2,3,…,n.

, sau

Definiția 2. Două matrice
Și
se numesc aceeași dimensiune egal, dacă acestea coincid element cu element, i.e. =,i = 1,2,3,…,m, j = 1,2,3,…,n.

Folosind matrice, este ușor de înregistrat unele dependențe economice, de exemplu, tabele de distribuție a resurselor pentru anumite sectoare ale economiei.

Definiția 3. Dacă numărul de rânduri ale unei matrice coincide cu numărul coloanelor acesteia, i.e. m = n, atunci se numește matricea ordine pătratăn, in caz contrar dreptunghiular.

Definiția 4. Tranziția de la matricea A la matricea A m, în care rândurile și coloanele sunt schimbate menținând ordinea, se numește transpunere matrici.

Tipuri de matrice: pătrat (dimensiunea 33) -
,

dreptunghiular (dimensiune 25) -
,

diagonala -
, singur -
, zero -
,

matrice-rând -
, matrice-coloană -.

Definiția 5. Elementele unei matrice pătrate de ordinul n cu aceiași indici se numesc elemente ale diagonalei principale, adică. acestea sunt elementele:
.

Definiția 6. Elementele unei matrice pătrate de ordinul n se numesc elemente ale diagonalei secundare dacă suma indicilor lor este egală cu n + 1, adică. acestea sunt elementele: .

1.2. Operații pe matrice.

1 0 . Cantitate două matrice
Și
de aceeași dimensiune se numește matrice C = (cu ij), ale cărei elemente sunt determinate de egalitatea cu ij = a ij + b ij, (i = 1,2,3,…,m, j = 1, 2,3,…,n).

Proprietățile operației de adunare a matricei.

Pentru orice matrice A, B, C de aceeași dimensiune, sunt valabile următoarele egalități:

1) A + B = B + A (comutativitate),

2) (A + B) + C = A + (B + C) = A + B + C (asociativitate).

2 0 . Munca matrici
pe număr  numită matrice
aceeași dimensiune ca matricea A și b ij =  (i = 1,2,3,…,m, j = 1,2,3,…,n).

Proprietățile operației de înmulțire a unei matrice cu un număr.

(A) = ()A (asociativitatea înmulțirii);

(A+B) = A+B (distributivitatea înmulțirii relativ la adunarea matricei);

(+)A = A+A (distributivitatea înmulțirii relativ la adunarea numerelor).

Definiția 7. Combinație liniară de matrici
Și
de aceeași dimensiune se numește expresie de forma A+B, unde  și  sunt numere arbitrare.

3 0 . Produsul A  În matrice A și, respectiv, B de dimensiunea mn și nk, se numesc matrice C de dimensiunea mk, astfel încât elementul cu ij este egal cu suma produselor elementelor din rândul i. a matricei A și a j-a coloană a matricei B, adică. cu ij = a i 1 b 1 j +a i 2 b 2 j +…+a ik b kj .

Produsul AB există numai dacă numărul de coloane ale matricei A coincide cu numărul de rânduri ale matricei B.

Proprietățile operației de înmulțire a matricei:

(AB)C = A(BC) (asociativitate);

(A+B)C = AC+BC (distributivitatea în raport cu adăugarea matricei);

A(B+C) = AB+AC (distributivitatea în raport cu adăugarea matricei);

AB  BA (nu comutativ).

Definiția 8. Matricele A și B, pentru care AB = BA, se numesc navetă sau navetă.

Înmulțirea unei matrice pătrate de orice ordin cu matricea de identitate corespunzătoare nu schimbă matricea.

Definiția 9. Transformări elementare Următoarele operații se numesc matrice:

Schimbați două rânduri (coloane).

Înmulțirea fiecărui element al unui rând (coloană) cu un alt număr decât zero.

Adăugarea elementelor unui rând (coloană) a elementelor corespunzătoare ale altui rând (coloană).

Definiția 10. Matricea B obținută din matricea A folosind transformări elementare se numește echivalent(notat cu BA).

Exemplul 1.1. Găsiți o combinație liniară de matrice 2A–3B dacă

,
.

,
,

.

Exemplu 1.2. Aflați produsul matricelor
, Dacă

.

Rezolvare: deoarece numărul de coloane din prima matrice coincide cu numărul de rânduri din a doua matrice, atunci produsul matricelor există. Ca rezultat, obținem o nouă matrice
, Unde

Ca rezultat obținem
.

Curs 2. Determinanti. Calculul determinanților de ordinul doi și trei. Proprietățile determinanțilorn-a ordine.

O matrice este un tabel dreptunghiular de numere cu o anumită cantitate m linii şi cu o anumită sumă n coloane. Numerele mȘi n sunt numite Comenzi sau dimensiuni matrici.

Matrice de comandă m×n se scrie sub forma:

sau (i= 1,2 ,...m; j= 1,2 ,...n).

Numerele a ij cele incluse în această matrice se numesc elementele acesteia. În înregistrare a ij primul indice iînseamnă numărul liniei și al doilea index j- numărul coloanei.

Rândul matricei

Dimensiunea matricei 1 ×n, adică format dintr-o linie se numește matrice-rând. De exemplu:

Coloana matricei

Dimensiunea matricei m×1, adică format dintr-o coloană se numește matrice-coloană. De exemplu

Matrice nulă

Dacă toate elementele unei matrice sunt egale cu zero, atunci matricea este numită matrice zero. De exemplu

Matrice pătrată

Matrice A Ordin m×n numit matrice pătrată dacă numărul de rânduri și coloane este același: m=n. Număr m=n numit în ordine matrice pătrată. De exemplu:

Diagonala principală a matricei

a 11 , a 22 ,..., a nn formă diagonala principală matrici. De exemplu:

Când m×n-elementele matricei a ii (i= 1,2 ,...,min(m,n)) de asemenea forma diagonala principală. De exemplu:

Elementele situate pe diagonala principală sunt numite elementele diagonale principale sau pur și simplu elemente diagonale .

Diagonala laterală a matricei

Elemente la locul lor a 1n , a 2n-1 ,..., a n1 formă diagonală laterală matrici. De exemplu:

Matricea diagonală

Matricea pătrată se numește diagonală, dacă elementele situate în afara diagonalei principale sunt zero. Exemplu de matrice diagonală:

Matrice de identitate

Matrice pătrată n Se numește ordinul --lea, care are unele pe diagonala principală și toate celelalte elemente sunt egale cu zero matrice de identitateși este notat cu E sau E n, unde n- ordinea matricei. Matricea de identitate de ordinul 3 are următoarea formă:

Urmă matriceală

Suma principalelor elemente diagonale ale matricei A numit Următorul matricea si se noteaza cu Sp A sau Tr A. De exemplu:

Matricea triunghiulară superioară

Se numește o matrice pătrată de ordinul n×n triunghiular superior matrice dacă toate elementele matricei situate sub diagonala principală sunt egale cu zero, i.e. a ij =0, în fața tuturor i>j. De exemplu:

Matrice triunghiulară inferioară

Matrice de ordine pătrată n×n numit triunghiular inferior matrice dacă toate elementele matricei situate deasupra diagonalei principale sunt egale cu zero, adică. a ij =0, în fața tuturor i . De exemplu:

Rânduri de matrice A formă spațiu de linii R(A T).

Coloane de matrice A formă spațiu coloană matrici și sunt notate cu R(A).

Kernel sau spațiu nul al unei matrice

Mulțimea tuturor soluțiilor ecuației Ax=0, Unde A.m X n-matrice, X- vector lungime n- forme spațiu nul sau miez matrici Ași este notat cu Ker(A) sau N / A).

Matrice opusă

Pentru orice matrice A există o matrice opusă -A astfel încât A+(-A)=0. Evident, ca matrice -A ar trebui să luați matricea (-1)A, ale căror elemente diferă de elemente A familiar.

Matrice desimetrică (symetrică).

O matrice pătrată se numește simetrică oblică dacă diferă de matricea sa transpusă cu un factor de -1:

Într-o matrice simetrică oblică, oricare două elemente situate simetric față de diagonala principală diferă între ele printr-un factor de -1, iar elementele diagonale sunt egale cu zero.

Un exemplu de matrice oblică-simetrică:

Diferența de matrice

Prin diferenta C două matrice AȘi B de aceeași dimensiune este determinată de egalitate

Pentru a indica diferența dintre două matrici, se utilizează următoarea notație:

Gradul de matrice

Fie o matrice pătrată de dimensiune n×n. Apoi, gradul matricei este definit după cum urmează:

unde E este matricea identității.

Din proprietatea asociativă a înmulțirii rezultă:

Unde p,q- numere întregi nenegative arbitrare.

Matrice simetrică (simetrică).

Matrice care satisface condiția A=A T se numește matrice simetrică.

Pentru matricele simetrice egalitatea este valabilă:

a ij =a ji ; i=1,2,...n, j=1,2,...n

Acest manual vă va ajuta să învățați cum să lucrați operatii cu matrici: adunarea (scăderea) matricelor, transpunerea unei matrice, înmulțirea matricelor, aflarea matricei inverse. Tot materialul este prezentat într-o formă simplă și accesibilă, sunt date exemple relevante, astfel încât chiar și o persoană nepregătită poate învăța cum să efectueze acțiuni cu matrice. Pentru automonitorizare și autotestare, puteți descărca gratuit un calculator matrice >>>.

Voi încerca să minimizez calculele teoretice; în unele locuri sunt posibile explicații „pe degete” și utilizarea unor termeni neștiințifici. Iubitori de teorie solidă, vă rugăm să nu vă implicați în critici, sarcina noastră este invata sa efectuezi operatii cu matrici.

Pentru pregătirea SUPER FAST pe tema (cine este „pe foc”) există un curs intensiv pdf Matrice, determinant și test!

O matrice este un tabel dreptunghiular al unora elemente. La fel de elemente vom lua în considerare numerele, adică matrice numerice. ELEMENT este un termen. Este indicat să rețineți termenul, va apărea des, nu întâmplător am folosit font aldine pentru a-l evidenția.

Desemnare: matricele sunt de obicei notate cu majuscule latine

Exemplu: Luați în considerare o matrice de două câte trei:

Această matrice este formată din șase elemente:

Toate numerele (elementele) din interiorul matricei există singure, adică nu se pune problema vreunei scăderi:

Este doar un tabel (set) de numere!

De asemenea, vom fi de acord nu rearanja numere, dacă nu se specifică altfel în explicații. Fiecare număr are propria sa locație și nu poate fi amestecat!

Matricea în cauză are două rânduri:

si trei coloane:

STANDARD: atunci când vorbim despre dimensiunile matricei la început indicați numărul de rânduri și abia apoi numărul de coloane. Tocmai am defalcat matricea de două câte trei.

Dacă numărul de rânduri și coloane ale unei matrice este același, atunci matricea este numită pătrat, De exemplu: – o matrice de trei câte trei.

Dacă o matrice are o coloană sau un rând, atunci se mai numesc și astfel de matrici vectori.

De fapt, conceptul de matrice îl cunoaștem încă de la școală; luați în considerare, de exemplu, un punct cu coordonatele „x” și „y”: . În esență, coordonatele unui punct sunt scrise într-o matrice una câte două. Apropo, iată un exemplu de ce contează ordinea numerelor: și sunt două puncte complet diferite pe plan.

Acum să trecem la studii operatii cu matrici:

1) Primul act. Eliminarea unui minus din matrice (introducerea unui minus în matrice).

Să revenim la matricea noastră . După cum probabil ați observat, există prea multe numere negative în această matrice. Acest lucru este foarte incomod din punctul de vedere al efectuării diferitelor acțiuni cu matricea, este incomod să scrieți atât de multe minusuri și pur și simplu arată urât în ​​design.

Să mutăm minusul în afara matricei prin schimbarea semnului fiecărui element al matricei:

La zero, după cum înțelegeți, semnul nu se schimbă; zero este zero și în Africa.

Exemplu invers: . Arată urât.

Să introducem un minus în matrice prin schimbarea semnului fiecărui element al matricei:

Ei bine, a ieșit mult mai frumos. Și, cel mai important, va fi MAI UȘOR să efectuați orice acțiuni cu matricea. Pentru că există un astfel de semn popular matematic: cu cât mai multe minusuri, cu atât mai multe confuzii și erori.

2) Actul doi. Înmulțirea unei matrice cu un număr.

Exemplu:

Este simplu, pentru a înmulți o matrice cu un număr, ai nevoie fiecare element de matrice înmulțit cu un număr dat. În acest caz - un trei.

Un alt exemplu util:

– înmulțirea unei matrice cu o fracție

Mai întâi să ne uităm la ce să facem NU ESTE NEVOIE:

NU ESTE NEVOIE să introduceți o fracție în matrice; în primul rând, complică doar acțiunile ulterioare cu matricea și, în al doilea rând, îngreunează profesorul să verifice soluția (mai ales dacă – răspunsul final al sarcinii).

Si in special, NU ESTE NEVOIEîmpărțiți fiecare element al matricei la minus șapte:

Din articol Matematică pentru manechin sau de unde să încep, ne amintim că la matematica superioară se încearcă să evite fracțiile zecimale cu virgule în toate modurile posibile.

Singurul lucru este preferabil Ce trebuie să faceți în acest exemplu este să adăugați un minus la matrice:

Dar dacă numai TOATE elementele matricei au fost împărțite la 7 fără urmă, atunci ar fi posibil (și necesar!) să se împartă.

Exemplu:

În acest caz, puteți TREBUIE SAînmulțiți toate elementele matricei cu , deoarece toate numerele matricei sunt divizibile cu 2 fără urmă.

Notă: în teoria matematicii de învățământ superior nu există conceptul de „diviziune”. În loc să spuneți „acest împărțit cu asta”, puteți spune întotdeauna „acest înmulțit cu o fracție”. Adică împărțirea este un caz special de înmulțire.

3) Actul trei. Matrix Transpose.

Pentru a transpune o matrice, trebuie să scrieți rândurile acesteia în coloanele matricei transpuse.

Exemplu:

Transpune matricea

Există un singur rând aici și, conform regulii, trebuie scris într-o coloană:

– matrice transpusă.

O matrice transpusă este de obicei indicată printr-un superscript sau un prim în dreapta sus.

Exemplu pas cu pas:

Transpune matricea

Mai întâi rescriem primul rând în prima coloană:

Apoi rescriem a doua linie în a doua coloană:

Și, în sfârșit, rescriem al treilea rând în a treia coloană:

Gata. În linii mari, transpunerea înseamnă întoarcerea matricei pe o parte.

4) Actul patru. Suma (diferența) matricelor.

Suma matricelor este o operație simplă.
NU TOATE MATRICILE POT FI POLIATE. Pentru a efectua adunarea (scăderea) matricelor, este necesar ca acestea să aibă ACEEAȘI DIMENSIUNE.

De exemplu, dacă se dă o matrice două câte două, atunci aceasta poate fi adăugată numai cu o matrice două câte două și nu alta!

Exemplu:

Adăugați matrici Și

Pentru a adăuga matrice, trebuie să adăugați elementele corespunzătoare ale acestora:

Pentru diferența de matrice regula este similară, este necesar să se găsească diferența elementelor corespunzătoare.

Exemplu:

Găsiți diferența de matrice ,

Cum poți rezolva mai ușor acest exemplu, ca să nu te încurci? Este recomandabil să scăpați de minusurile inutile; pentru a face acest lucru, adăugați un minus la matrice:

Notă: în teoria matematicii de învățământ superior nu există conceptul de „scădere”. În loc să spuneți „scădeți acest lucru din asta”, puteți spune întotdeauna „adăugați un număr negativ la acesta”. Adică scăderea este un caz special de adunare.

5) Actul cinci. Înmulțirea matricei.

Ce matrice pot fi multiplicate?

Pentru ca o matrice să fie înmulțită cu o matrice, este necesar astfel încât numărul de coloane de matrice să fie egal cu numărul de rânduri de matrice.

Exemplu:
Este posibil să înmulțim o matrice cu o matrice?

Aceasta înseamnă că datele matricei pot fi multiplicate.

Dar dacă matricele sunt rearanjate, atunci, în acest caz, înmulțirea nu mai este posibilă!

Prin urmare, înmulțirea nu este posibilă:

Nu este atât de rar să întâlniți sarcini cu un truc, atunci când elevului i se cere să înmulțească matrici, a căror înmulțire este evident imposibilă.

Trebuie remarcat faptul că în unele cazuri este posibilă multiplicarea matricelor în ambele moduri.
De exemplu, pentru matrice, și înmulțirea și înmulțirea sunt posibile